De Broglie Wavelength

Question 3.

Use Maple, to calculate the de Broglie wavelengths of the following.

(a) A nitrogen molecule at room temperature. Use the equipartition principle to help. 

The equipartition principle states that at thermal equilibrium the amount of energy is equal to ½*k*T for a gas, where k is the Boltzmann constant. 

We set our constants in Maple using room temperature at 23°C and m is the mass of nitrogen:

Planck Constant

>

Boltzmann Constant

>

Room Temp.

>

Mass of Nitrogen

>

Then we find KE using the equipartition principle that was explained above:

>

Finally solve for the wavelength using the equation from question 2:

>

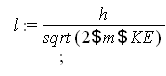
This shows the wavelength in meters of a nitrogen molecule at room temperature. 

(b) A 1.5 g bullet traveling at 650 mi/hr.

Here we convert mi/hr to m/s:

>

And set this to the variable v:

>

Change g to kg:

>

And set to variable m:

>

Using the equation for kinetic energy we figure out KE:

>

Finally determine the wavelength using the equation from question 2:

>

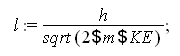
This answer shows us the wavelength of a 1.5 g bullet when it is traveling at 650 mi/hr.  The wavelength of the bullet is even smaller than that of the nitrogen molecule at room temperature which means although the bullet has a wavelength there is no way we could see it with the human eye.