Modeling Successional Changes in a Raised Mire

Model due to J.N.R. Jeffers

http://www.icsu-scope.org/downloadpubs/scope34/chapter6.html

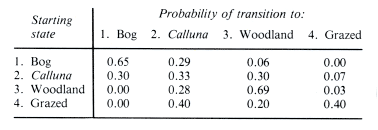
Raised mires frequently show interesting successional changes as a result of increased drainage, and Figure 17 gives the estimated probabilities for the transitions between four possible states of a raised mire over a period of 20 years. State 1 represents the wettest facies dominated by Sphagnum, with Calluna, Erica tetralix and Eriophorum as the major vascular plant components. State 2 represents a drier facies, with a Calluna-Cladonia association and seedlings of Betula and Pinus sylvestris, the more mature woodland of State 3 having a typical Vaccinium myrtillus community with hypnaceous mosses. State 4 represents disturbance due to grazing by large herbivores of the drier facies, leading to the establishment of a Molinia-Pteridium-dominated association.

Thus, areas which start as typical bog vegetation have a probability of 0.65 of remaining as bog vegetation at the end of the 20-year time-step, and probabilities of 0.29 and 0.06 respectively of becoming Calluna-dominated and woodland. Areas which start as Calluna-dominated have roughly equal probabilities of remaining in the same state, returning to bog vegetation because of fluctuations in the water table, or of becoming woodland: they have a small (0.07) probability of being subjected to sporadic grazing. Woodland areas have a 0.69 probability of remaining as woodland, a probability of 0.28 of returning to Calluna because of deaths of trees, and, again, a small (0.03) probability of being subjected to sporadic grazing. The grazed areas have an equal probability of being subjected to further grazing and of returning to a Calluna-dominated vegetation, and a small (0.20) probability of becoming woodland because of the growth of ungrazed seedlings.

Figure 17. Transitional probabilities for successional changes in a raised mire (time step = 20 years)

None of the states, therefore, are absorbing or members of a closed set, and the matrix represents a transition from the bog vegetation to woodland, with an imposed disturbance due to grazing. However, although there can be a return from the Calluna-dominated vegetation to bog vegetation because of fluctuations in the water table, there is no immediate return from woodland to bog vegetation. Where there are no absorbing states, the Markov process is known as an ergodic Markov chain, and the full implications of this model can be exploited by an analysis of the transition matrix.