The activity of constructing, analyzing, interpreting, and evaluating mathematical models is the central process in applying mathematics to real problems.

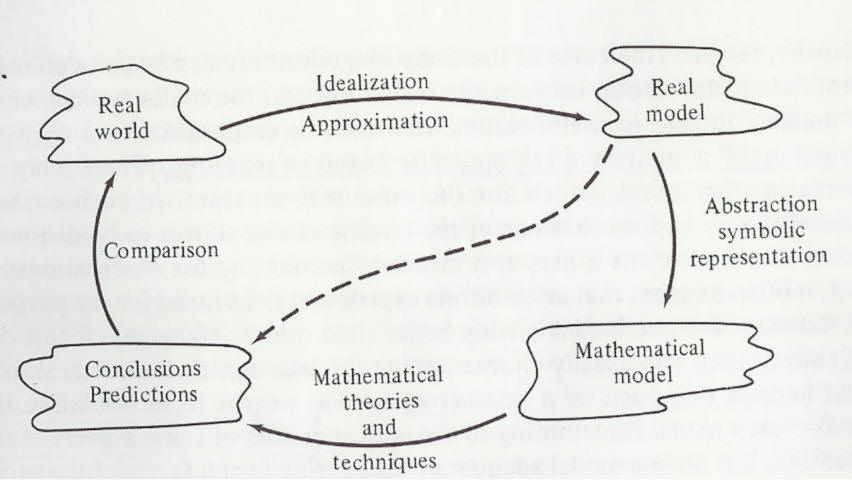
An original problem arises in the real world and is associated with some phenomenon of particular interest.  Our task is to formulate a mathematical description of the phenomenon so that we may make predictions, choose an optimal course of action, or better understand the phenomenon.

The Mathematical Modeling Process

A real model is a collection of statements about real objects, relations, and processes which is obtained by observation, identification, simplification, and approximation.

A mathematical model is an axiom system which is obtained by abstracting and quantifying the essential elements of a real model.

A logical model is an association of (real) objects, relations, and processes with the undefined terms of an axiom system so that the axioms become verifiable statements.

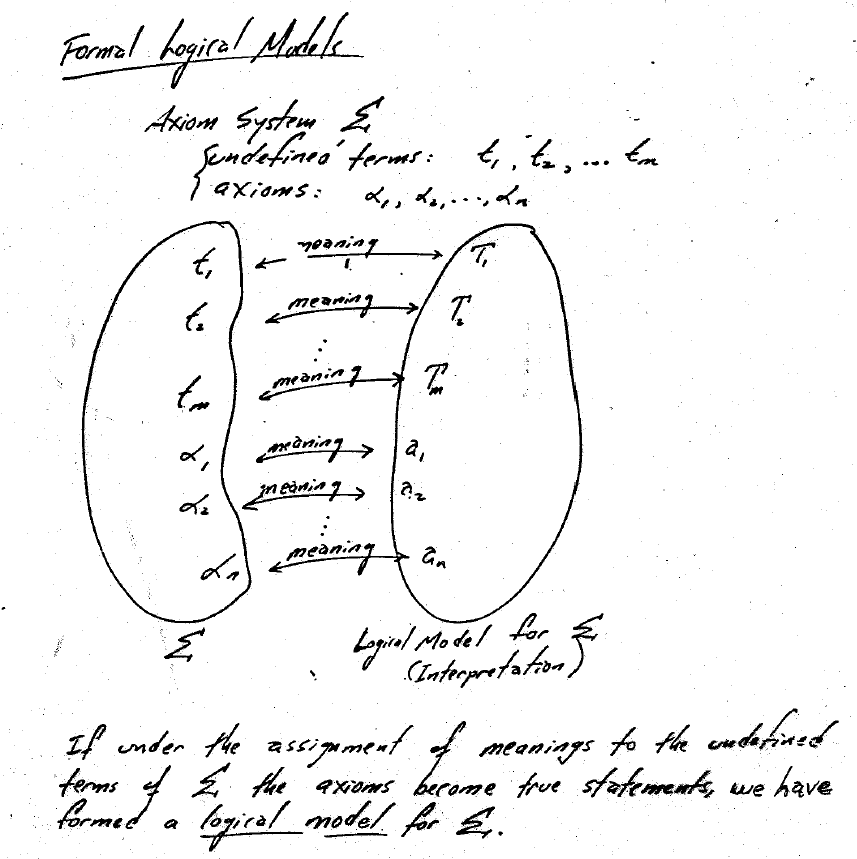
Mathematical (Logical) System, Σ

• An undelying language

• A deductive system (logic, set theory)

• A vocabulary of undefined words (objects, relations, operations)

• Axioms and definitions (accepted statements about the undefined words)

• Theorems (statements that can be proved; theory for Σ)

A consistent system Σ contains no contradictory statements.  (verified by models)