Polya's Four Step Problem Solving Process

Step 1: Understand the Problem

¨ Do you understand all the words?

¨ Can you restate the problem in your own words?

¨ Do you know what is given?

¨ Do you know what the goal is?

¨ Is there enough information?

¨ Is there extraneous information?

¨ Is this problem similar to another problem you have solved?

Step 2: Devise a Plan

Can one (or more) of the following strategies (heuristics) be used? (A strategy is defined as an artful means to an end.)

1. Guess and test.	12. Work backwards
2. Use a variable.	13. Use cases.
3. Draw a picture.	14. Solve an equation.
4. Look for a pattern.	15. Look for a formula.
5. Make a list.	16. Do a simulation.
6. Solve a simpler problem.	17. Use a model.
7. Draw a diagram.	18. Use dimensional analysis.
8. Use direct reasoning.	19. Identify subgoals.
9. Use indirect reasoning.	20. Use coordinates.
10. Use properties of numbers.	21.Use symmetry.
11. Solve an equivalent problem.

Step 3: Carry Out the Plan

¨ Implement the strategy or strategies that you have chosen until the problem is solved or until a new course of action is suggested.

¨ Give yourself a reasonable amount of time in which to solve the problem. If your are not successful, seek hints from others or put the problem aside for a while. (You may have a flash of insight when you least expect it!)

¨ Do not be afraid to start over. Often, a fresh start and a new strategy will lead to success.

Step 4: Look Back

¨ Is your solution correct? Does your answer satisfy the statement of the problem?

¨ Can you see an easier solution?

¨ Can you see how you can extend your solution to a more general case?

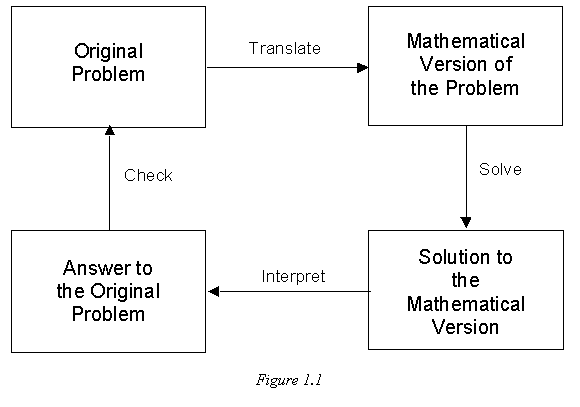
Usually, a problem is stated in words, either orally or written. Then, to solve the problem, one translates the words into an equivalent problem using mathematical symbols, solves this equivalent problem, and then interprets the answer. This process is summarized in Figure 1.1.