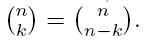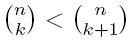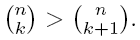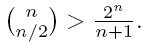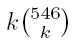Unimodality of the Binomial Coefficients
Pascal's triangle is a nice way to organize the binomial coefficients and its
structure has led mathematicians to discover many interesting properties
and identities involving the binomial coefficients. For instance, if we focus
on one particular row, say row n, we see that the binomial coefficients
steadily increase to a maximum value and then decrease steadily (to the
first value of that row). A sequence that has this property is said to be
unimodal. If we were to plot the terms of a unimodal sequence we would
see that they follow a bell-like curve.
Formally, we say that a sequence a0, a1, a2, ... ,
an is unimodal if there exist
indices i, j such that
 Our goals in this lab are to prove that the sequence of binomial coefficients
is unimodal and to establish bounds for the largest term in the sequence
when n is even.
Our goals in this lab are to prove that the sequence of binomial coefficients
is unimodal and to establish bounds for the largest term in the sequence
when n is even.
Exercises
- Use the Zn applet to the right to see that Pascal's
triangle is symmetric
(make sure to pick a very large modulus, say 1000, as
the binomial coefficients grow very quickly).
Show that
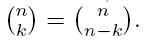
- Use the applet to see that each row of Pascal's triangle
has a maximum (and that it is achieved at least once). What is
the parity of the rows that have the maximum value occurring only
once? twice?
- Show that if k < (n - 1)/2, then
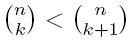 and that if k > (n - 1)/2, then
and that if k > (n - 1)/2, then
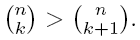 What happens if k = (n - 1)/2?
What happens if k = (n - 1)/2?
- Show that
 (Hint: Use the binomial theorem
to expand (x + 1)n and then let x = 1.) Use the above identity to
show that
(Hint: Use the binomial theorem
to expand (x + 1)n and then let x = 1.) Use the above identity to
show that

- Show that
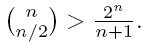 (Hint: What is 2n/(n+1), the average of?)
(Hint: What is 2n/(n+1), the average of?)
- Find the value of k for which
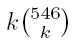 is largest.
is largest.