Cryptology

From before the time of Julius Caesar up until today, secret messages have been sent. Today more than ever, ciphers are important. For example, unencrypted sensitive information sent via the internet is easy prey for those that would like to steal your assets or identity (or both).

The purpose of this lab is to explore ciphers of the form

C ≡ aP + b (mod 26),
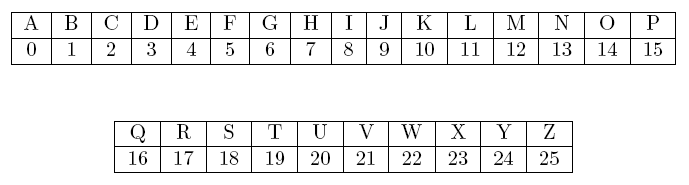
where P is a plaintext character, gcd(a, 26) = 1, b is any integer, and C is a ciphertext character. We use letters from the English language as our plaintext characters and we assign each letter an integer from 0 to 25, as shown below.
As an example of such a cipher, we consider a = 5 and b = 12. Suppose that we would like to encipher the plaintext message
I LOVE PASCALS TRIANGLE.
First we break the plaintext message into blocks of five letters – this insures that common words such as of and the are not recognized. Broken into groups of five letters, our original message becomes
ILOVE PASCA LSTRI ANGLE.
Converting the letters into their integer equivalents, we obtain
8 11 14 21 4     15 0 18 2 0     11 18 19 17 8     0 13 6 11 4.
Using the cipher C ≡ 5P + 12 (mod 26), this becomes
0 15 4 13 6     9 12 24 22 12     15 24 3 19 0     12 25 16 15 6.
Translating back to letters, we get
APENG JMYWM PYDTA MZQPG.

The above calculations can be carried out using the group calculator or using the Zn applet. To use the Zn applet, set n to 26 and use 5 and 12 as the seeds for the triangle (make sure to enter 5 on the left and 12 on the right). The second residue in the mth row will be the result of applying our cipher (a = 5 and b = 12) to m, where 0 <= m <= 25.

Exercises

    Zn Applet
  1. Why is the second residue in the mth row of the triangle generated by 5 and 12 the result of applying the cipher with a = 5 and b = 12 to m, where 0 <= m <= 25?
  2. Which transformation will decipher the ciphertext message
    APENG JMYWM PYDTA MZQPG?
    Is such a transformation unique? Why or why not?
  3. Encipher the message
    DRINK ENOUGH COFFEE
    using the cipher C ≡ 9P + 22 (mod 26).
  4. Decipher the message
    UEYDP CVMTU PGYY
    which was enciphered using the cipher C ≡ 17P + 13 (mod 26).
  5. Find the cipher that results by applying the cipher C ≡ 9P + 22 (mod 26) to the output of the cipher C ≡ 17P + 13 (mod 26). Show that the resulting cipher is of the form C ≡ aP + b (mod 26) where gcd(a, 26) = 1.