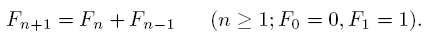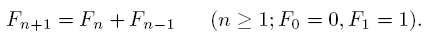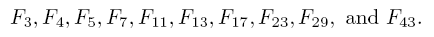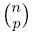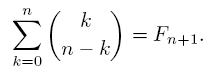Fibonacci Primes
The Fibonacci numbers are a famous sequence of numbers, generally attributed
to Leonardo of Pisa, which are given by the following recurrence
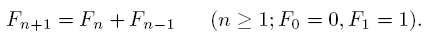
While it is true that the Fibonacci numbers can be found in Pascal's triangle
(sum the binomial coefficients on the back diagonals), the main purpose of
this lab is to explore the Fibonacci numbers which are prime.
It is not known whether or not there are infinitely many Fibonacci primes.
The first ten Fibonacci primes are
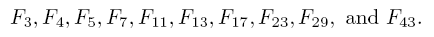 Except for F4, it is true that if Fn is prime,
then n is prime. The converse is
not true however. For example, F19 = 4181 = 37 x 113. To date, the largest
known Fibonacci prime is F81839. (For an up-to-date listing of Fibonacci
primes, check out Neil Sloane’s On-Line Encyclopedia of Integer Sequences.)
Except for F4, it is true that if Fn is prime,
then n is prime. The converse is
not true however. For example, F19 = 4181 = 37 x 113. To date, the largest
known Fibonacci prime is F81839. (For an up-to-date listing of Fibonacci
primes, check out Neil Sloane’s On-Line Encyclopedia of Integer Sequences.)
Exercises
- Prove that if 1 <= k <= n - 1, then
 if and only if n is prime. (Hint: To establish the necessary condition, prove its
contrapositive. That is, suppose that n is composite, let p be its
largest prime divisor, and then show that the binomial coefficient
if and only if n is prime. (Hint: To establish the necessary condition, prove its
contrapositive. That is, suppose that n is composite, let p be its
largest prime divisor, and then show that the binomial coefficient
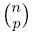 is not equal to 0 modulo n.)
is not equal to 0 modulo n.)
- Find the first six Fibonacci primes using the Fibonacci recurrence.
That is, F3 =?, F4 =?, etc.
- Use exercise 1 and the Zn applet to show that F13 is
prime.
- Is F2 prime? Use exercise 1 and the Zn applet to show
that F19 is not prime.
- Use induction to prove that
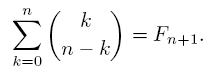
- Use induction to prove that if n >= 1, then gcd(Fn, Fn-1) = 1.
(Hint: gcd(a, b) = gcd(b, a - b)).