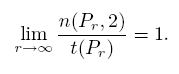How many binomial coefficients are even?
It is no accident that the mod 2 Pascal's triangle bears a strong resemblance
to Sierpinski's famous fractal called the gasket.

One can in fact think of the mod 2 triangle as a close relative to the gasket.
The proof of this fact requires quite a bit of advanced number theory, so its
proof will be omitted. (The interested reader may find a readable exposition
of this fact in [2].) The gasket is the result of an iterative process where one
starts with a filled-in equilateral triangle with side length s and removes the
middle equilateral triangle formed by connecting the midpoints of each pair
of sides. Proceed by removing the middle equilateral triangle in each of the
three smaller remaining filled-in equilateral triangles (each with side length
(1/2)s). Continuing this process indefinitely gives us the Sierpinski gasket.
An interesting question at this point is how much of the starting triangle
did we remove? To simplify calculations, letís suppose that the starting
triangle had area equal to 1. In the first step we removed a triangle that
had area 1/4. In the second step we removed three triangles, each with
area equal to 1/16. Thus the total removed area at this point is equal to
1/4 + 3/16. Continuing this process we see that the removed area is equal to
1/4 + 3/16 + 9/64 + ... = 1.
That is, the remaining structure has zero area!
What does this calculation tell us about Pascal's triangle? To answer this
question, first let Pr represent the first r rows of Pascal's triangle. Also
let n(Pr, 2) be the number of even binomial coefficients in Pr
and let t(Pr)
represent the total number of binomial coefficients in Pr. Then this result
tells us that
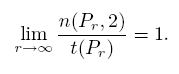 That is, most of the binomial coefficients in Pascalís triangle are even, a
surprising result. The exercises below ask you to see what else can be
learned by looking at Pascalís triangle modulo an odd prime.
That is, most of the binomial coefficients in Pascalís triangle are even, a
surprising result. The exercises below ask you to see what else can be
learned by looking at Pascalís triangle modulo an odd prime.
Exercises
- Use the applet to the right to graph the mod 3 triangle. Make
sure to color all of the nonzero residues the same (say black). The
picture you obtain will look like

- If the picture had infinite detail, like Sierpinskiís gasket, how
much area is taken away (i.e., colored red)?
- What does this imply about the number of binomial coefficients
that are divisible by 3?
- How many rows of Pascal's triangle do we have to take to insure
that the binomial coefficients that are divisible by 3 make up
approximately 1/2 of the triangle?
- Next use the applet to graph the mod 5 triangle.
Again, be sure to color all of the nonzero residues the same. The
picture you obtain will look like

- If the picture had infinite detail, like Sierpinskiís gasket, how
much area is taken away (i.e., colored red)?
- What does this imply about the number of binomial coefficients
that are divisible by 5?
- How many rows of Pascal's triangle do we have to take to insure
that the binomial coefficients that are divisible by 5 make up
approximately 1/2 of the triangle?
- Is what you found in exercises 1 and 2 true for larger primes? Can
you prove it? What does this say about Pascal's triangle?
A rigorous treatment of the results explored here can be found in [1].
References
[1] N. Fine, Binomial coefficients modulo a prime, Monthly 54 (1947), 589-92
[2] H-O. Peitgen, H. Jurgens, and D. Saupe , Chaos and Fractals: New
Frontiers of Science, 2nd ed., Springer-Verlag, New York, NY (2004).