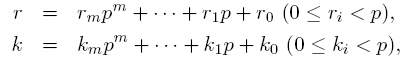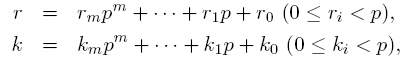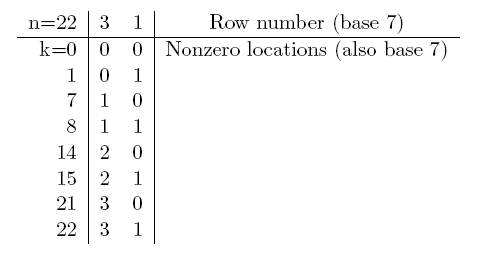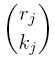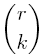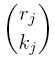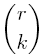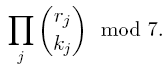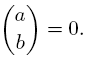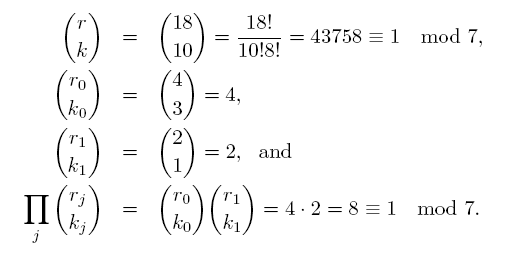The Lucas Correspondence Theorem
Introduction
Given a prime number p and integers r, k
such that r > 0 and 0 <= k <= r, we will write the base p
representations of r and k as follows:
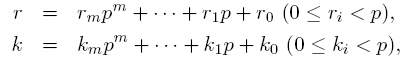
where m is chosen such that pm <= r < pm+1.
We will consider row r of Pascal's Triangle modulo p.
As an example, let p = 7 and r = 22; that is, we
will consider the 22nd row of Pascal's Triangle modulo 7:
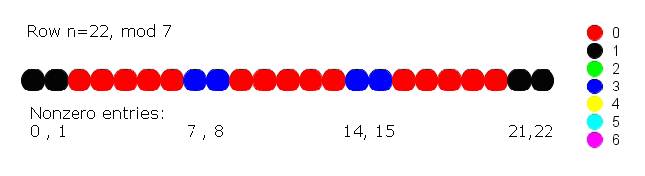
If we write the row number and the locations of the
non-zero entries, all in base 7 (including leading zeros,
if necessary), we get the following table:
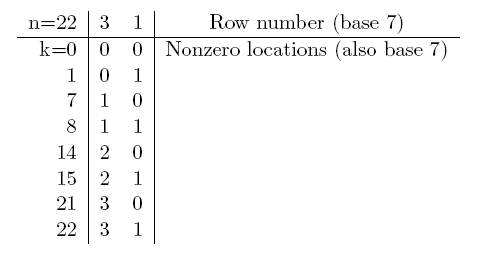
From examples such as this one, we wish to infer a method of
predicting the nonzero entries of row n of
Pascal's triangle modulo p.
Activity Instructions
- Following the above example, create similar tables for rows
14, 16, 18 and 20 of Pascal's triangle
modulo 7. In each case, what is the relationship between the base
p digits of the row number and
the base p digits of the locations of the nonzero entries?
When using this applet to graph Pascal's triangle modulo n you
will need to
- Change the n = box to your modulus.
- Place a 1 in one of the seed boxes and remove any entry in the other seed box.
Also, remember that the divider between the triangle and the color scheme
is moveable.
- For a few different values of k from row r = 18 of the
(mod 7) triangle, calculate the binomial coefficient
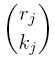 for each j. In each case, compare your results to the value of
for each j. In each case, compare your results to the value of
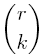 Write out your results.
Write out your results.
- For each of the examples you considered in
# 2, look for a connection between the values of
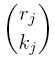 mod 7 and the value of
mod 7 and the value of
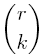 mod 7. In particular, consider the product
mod 7. In particular, consider the product
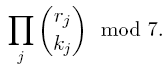 Keep in mind that when a < b,
Keep in mind that when a < b,
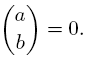 For example: If r = 18 = 247 and k = 10 = 137, then:
For example: If r = 18 = 247 and k = 10 = 137, then:
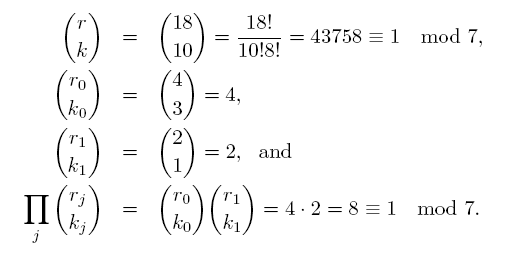 Come up with a conjecture about the connection between
Come up with a conjecture about the connection between

- Test your conjecture for some other prime moduli p and rows r.
(So far we’ve only really considered
p = 7 and r = 18.) Consider at least two other values of
p; for each of these, repeat the procedures
described in #1 and #2 above for at least two or three different rows
of Pascal's triangle modulo p.
Does your conjecture from # 3 seem to hold up? Do you think it is true in general?
- Look up the "Lucas Correspondence Theorem" on the internet.
(For example, you can find it on
http://mathworld.wolfram.com.)
Compare what you find to what you came up with in #3–4 above.
- Describe how the Lucas Correspondence Theorem reveals the locations of the zero versus
non-zero entries of Pascal's triangle modulo a prime p.