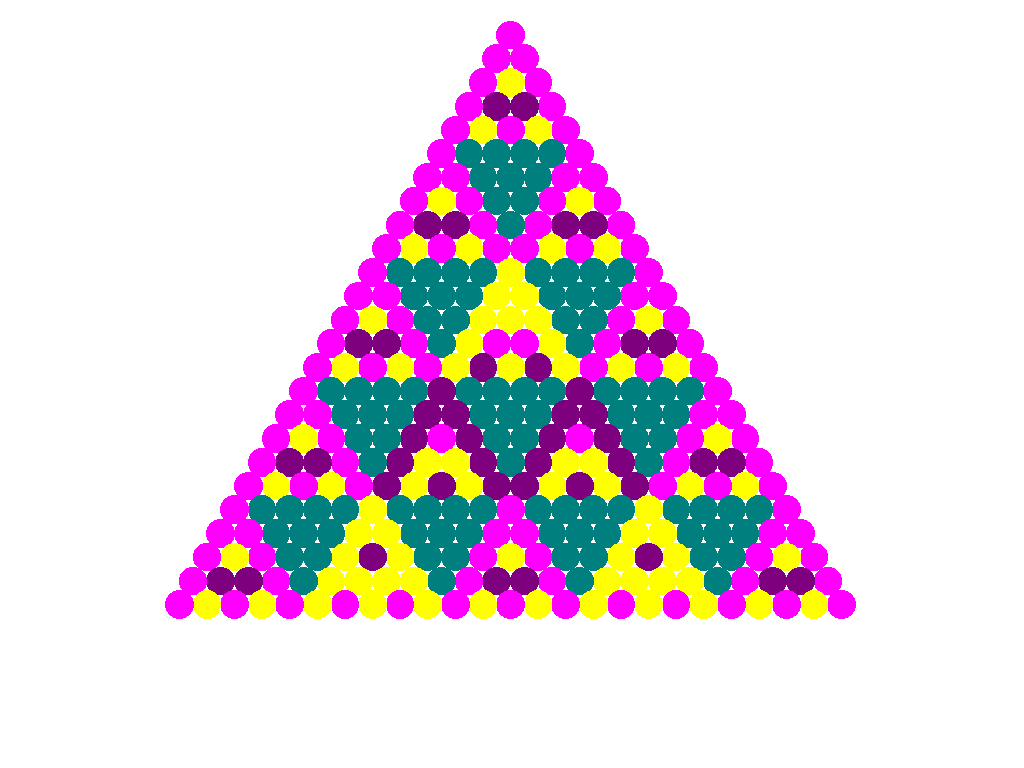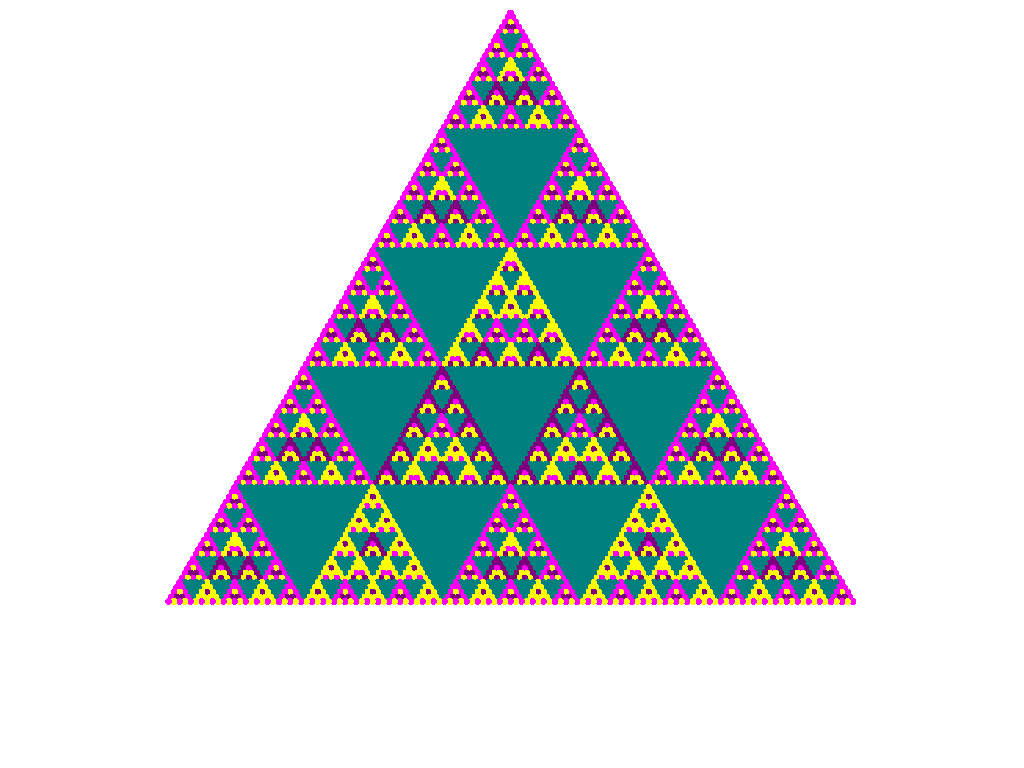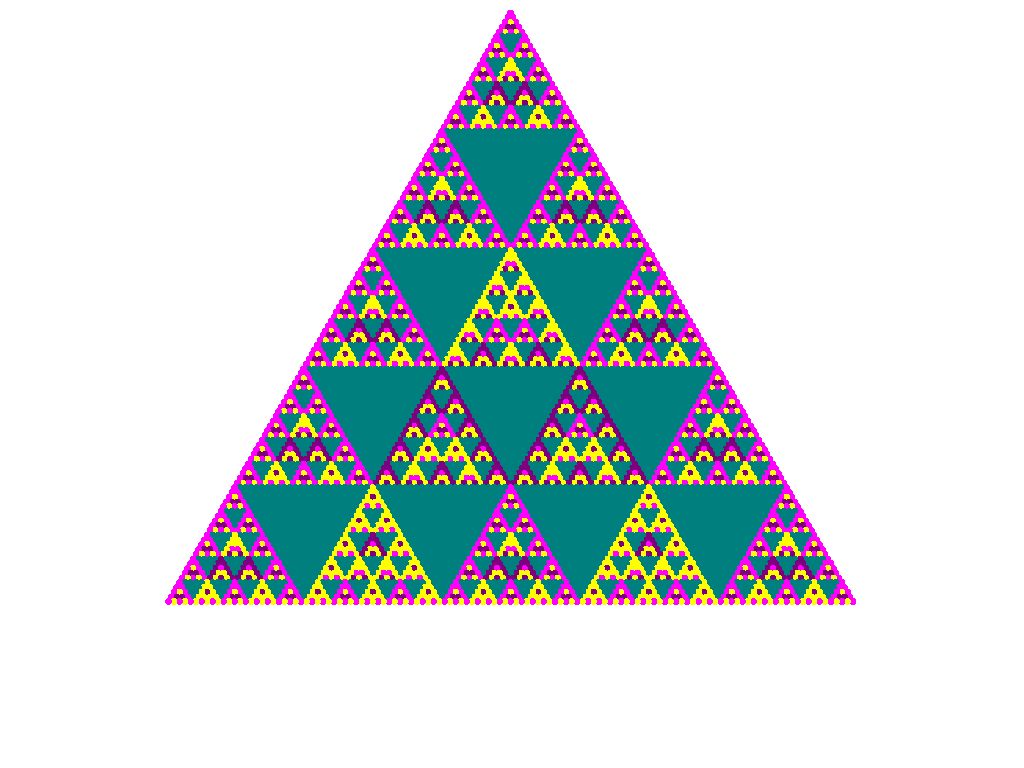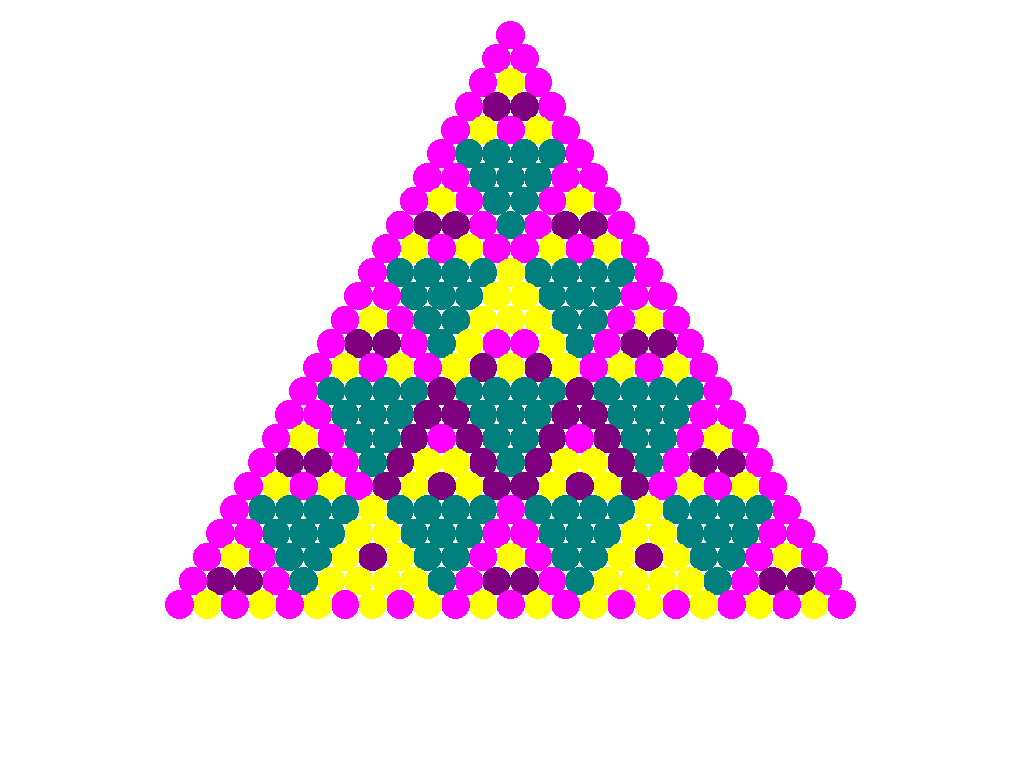What happens when you increase the number of rows in a PascGalois Triangle?

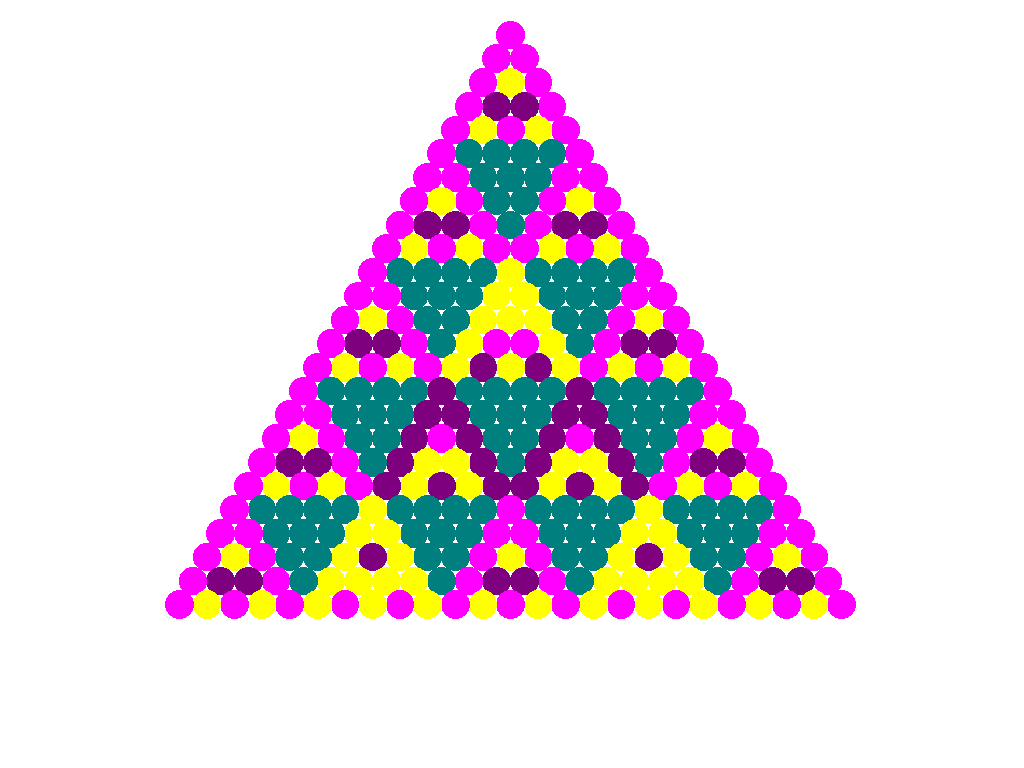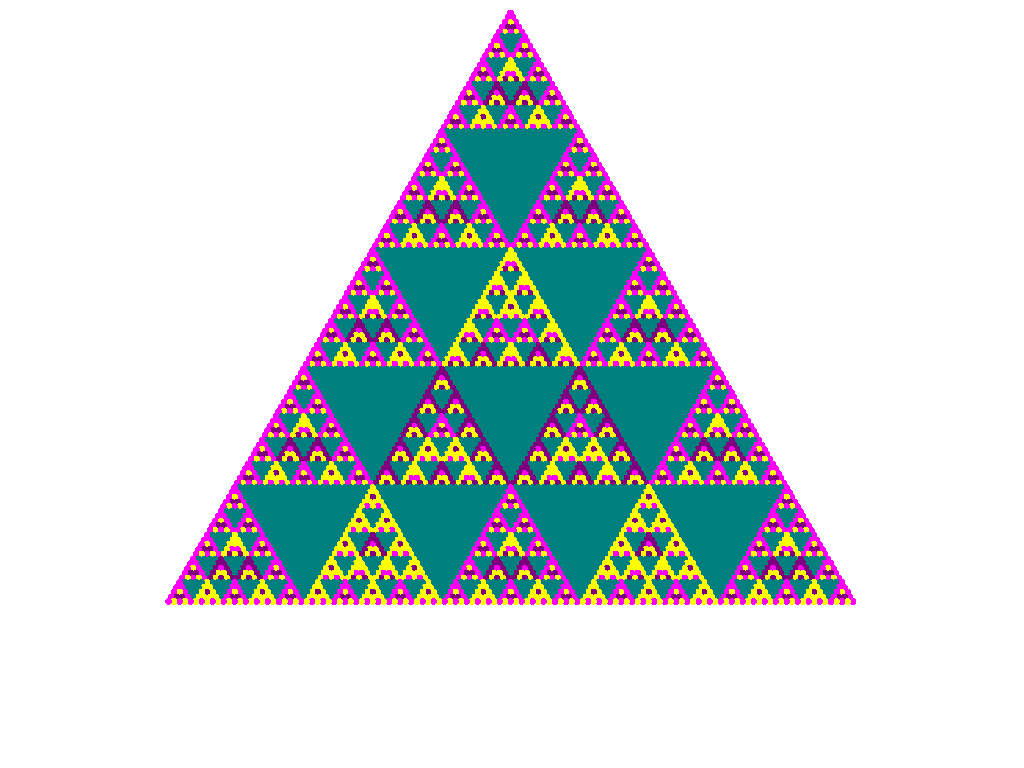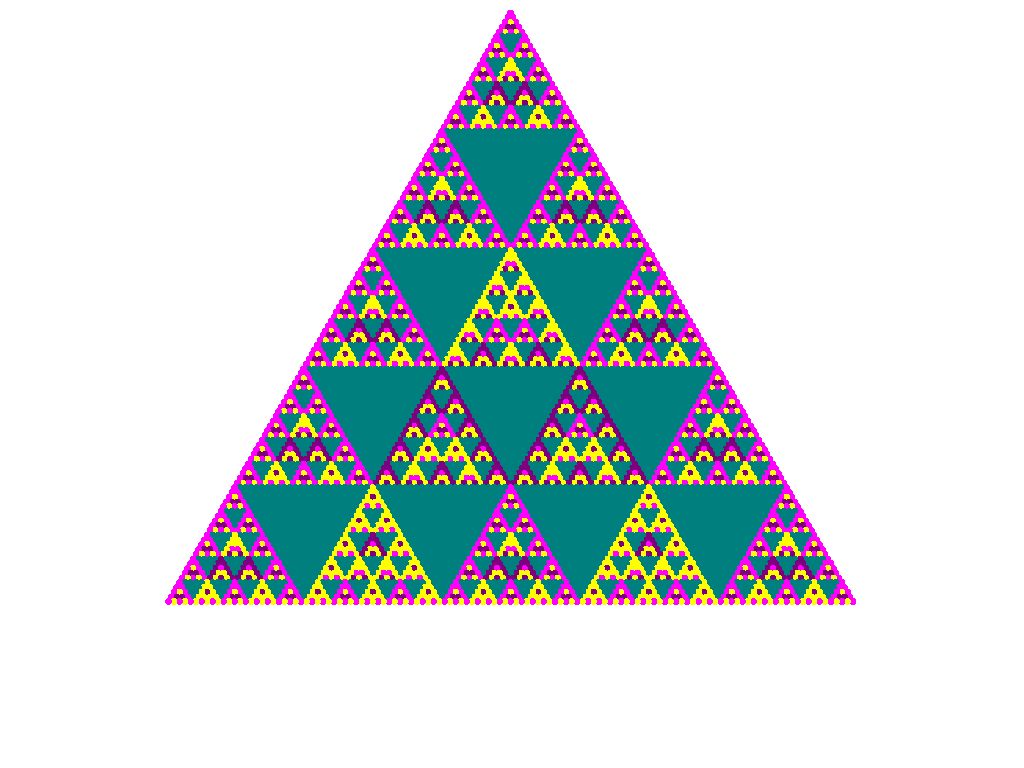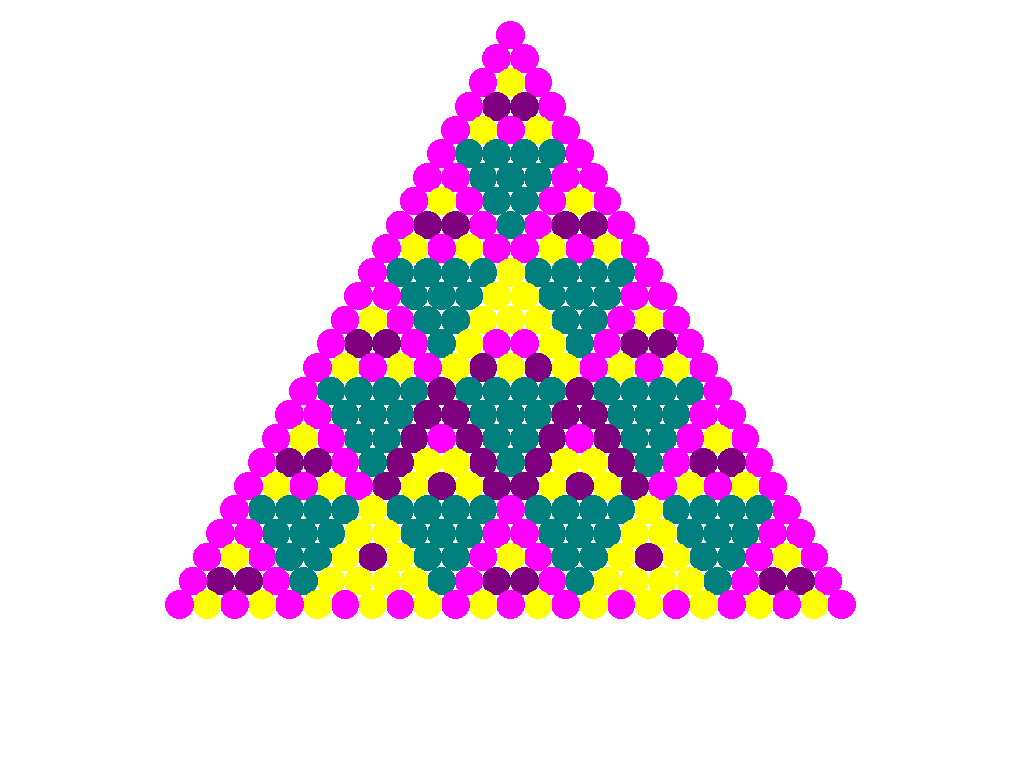
This animation shows Pascal's Triangles mod 3 where each triangle has either three times as many or a third as many rows as the previous one. Notice how the general structure or appearance of the triangle is preserved as you "zoom out".	This animation shows Pascal's Triangles mod 5 where each triangle has either five times as many or a fifth as many rows as the previous one. Notice how the general structure or appearance of the triangle is preserved as you "zoom out".
This animation shows the PascGalois Triangles for D4 ( standard construction) where each triangle has either twice as many or half as many rows as the previous one. Notice how the general structure or appearance of the triangle is preserved as you "zoom out".	This animation shows the PascGalois Triangles for D3 ( standard construction) where each triangle has either twice as many or half as many rows as the previous one. Notice how the general structure or appearance of the triangle is preserved as you "zoom out".

When something looks the same when you look at it on different scales, it is said to be self-similar. For example, imagine looking at a satellite image of a jagged coastline. Now consider looking at an image taken from an airplane of a smaller section of the same coastline. Finally, think of an image of the coastline taken from a tower nearby of a yet smaller section of the coast. Assuming the coast is natural and undeveloped, all three images would likely look pretty much the same. By changing the scale, you do not change the essential nature of the "curve" that would outline the coast. You can perform the same exercise, looking at snapshots taken at different distances for other images as well; for example think of the patterns in the growth of a fern or a tree. A single branch of a tree looks pretty much like a tree itself. These are all examples of a property called self-similarity that is found in geometric objects known as fractals. See [5, pp. 398-511], [6], and [7] for more information about fractals and fractal geometry. Fractals arise in an area of mathematics called Dynamical Systems or Chaos Theory which became very popular in 1980's. It continues to be a rich area of mathematics as these fractal patterns frequently better correspond to many things we see in nature than do the shapes (circles, triangles, rectangles, general polyhedra, etc.) that had previously been used to describe them. PascGalois Triangles exhibit their own kind of self-similarity and the tools that have been developed, like the notion of a fractal dimension, to study the self-similar structure of fractals can be modified to study them as well. This is one avenue of further study related to these images. (See [1] and [14] for more information)