|
Chapter 19 Lecture Notes
 Formulas: Formulas:
RS = R1 + R2 + ...
1/RP = 1/R1 + 1/R2 + ...
CP = C1 + C2 + ...
1/CS = 1/C1 + 1/C2 + ...
q = qo[1-e-t/(RC)]
q = qoe-t/(RC)
t = RC

Demonstrations:
- Marbles and tubes.
- Light bulbs in series and parallel
- Tungsten wire blowing out.
Resistors in a Circuit
A child's game of Marbles and Tubes illustrates the concepts of series and parallel. Series are in connected in a straight line and have the same current through them.
Parallel have the same voltage drop across them.
Series Wiring
Look at two resistors in series. The current going through each resistor is the same so
V = IR1 + IR2 = I(R1 + R2) = IRs
If they have the same current flowing through them, then they are in series.
 |
 |
|
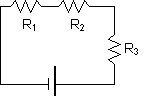 PROBLEM
: (a) What is the current flowing through a 3W, 6W, and 9W resistor in series when connected to a 12 V battery? (b) What is
the voltage drop across each resistor? PROBLEM
: (a) What is the current flowing through a 3W, 6W, and 9W resistor in series when connected to a 12 V battery? (b) What is
the voltage drop across each resistor?
(a) V = I(R1 + R2 + R3) = I(18W)
I = V/(18 W) = 12V/18W = .67 Amps
The equivalent resistance is 18 W which is greater than the resistance of any single resistor. We draw equivalent circuits with fewer resistors.
(b) Since V = IR and the current is the same for each one, the voltage drop across
each resistor is given as:
V1 = IR1 = (.67A)(3W) = 2 V
V2 = IR2 = (.67A)(6W) = 4 V
V3 = IR3 = (.67A)(9W) = 6 V
Note how V1 + V2 + V3 = 12 V which is the voltage across the battery.
|
|
|
Parallel Wiring
In a parallel circuit the voltage across each resistor is the same, so
I = I1 + I2 = V/R1 + V/R2 =V(1/R1 + 1/R2) = V(1/RP)
In general, 1/RP = 1/R1 + 1/R2 + 1/R3 + ...
 |
 |
|
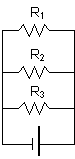 PROBLEM
: (a) What is the total current in a circuit if a 3W, 6W, and 9W resistor
are all connected in parallel to a 12 V battery? (b) What is the current in each resistor? PROBLEM
: (a) What is the total current in a circuit if a 3W, 6W, and 9W resistor
are all connected in parallel to a 12 V battery? (b) What is the current in each resistor?
(a) 1/RP = 1/R1 + 1/R2 + 1/R3 = 1/3W + 1/6W + 1/9W
1/RP = 11/18 W
RP = 18/11 W = 1.6 W
Note how the resistance of resistors in parallel is less than the resistance of any single resistor. (Draw equivalent circuits).
I = V/(1.6 W) = 12V/1.6W = 7.3 A
(b) For each resistor V = IR, and V is 12 V, so:
I1= V/R1 = 12V/3W = 4 A
I2= V/R2 = 12V/6W = 2 A
I3= V/R3 = 12V/8W = 1.3 A
Note how I1+ I2+I3= 7.3 Amps, which is the total current.
|
|
|
Parallel and Series Together (Equivalent Circuits)
If I have many resistors in parallel and in series, then I just take a step-by-step process to reduce this to an equivalent circuit.
 |
 |
|
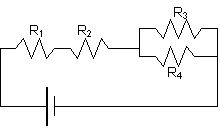 PROBLEM: What is the equivalent resistance of this circuit? PROBLEM: What is the equivalent resistance of this circuit?
R1 = 2W R2 = 4W
R3 = 5W R4 = 10W
First look at R3 and R4. These two resistors are
in parallel because any current flow has a choice of which resistor to go through. Thus,
Rp = (1/R3+1/R4)-1 = (1/5 + 1/10)-1 = 3.33W
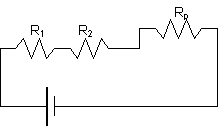 And we have that the starting circuit is equivalent to one that looks like the following.
Now we can easily see that R1,R2, and Rp are in series because any current must flow through each resistor (or resistor branch). And we have that the starting circuit is equivalent to one that looks like the following.
Now we can easily see that R1,R2, and Rp are in series because any current must flow through each resistor (or resistor branch).
RT = 2 + 4 + 3.33 = 9 W
|
|
|
 |
 |
|
PROBLEM: How many amps
run through a tungsten wire when it is hooked up in series to a 100-watt light bulb and 600-watt heater that are in parallel?
V2/R=100, So R=144W, For 600 W heater, R = 24 W.
With the light bulb in the circuit,V=IR, so I=0.83 A.
With the heater in the circuit:
V=IR 1/R = 1/R1 + 1/R2 = 1/144 + 1/24, so R=21 W.
V=IR, so I = 6 Amps.
|
|
|
We can put many resistors together and often still reduce them to a single equivalent resistor.
Show how you can rearrange the diagram. Use one like below with all resistors having the same resistance.
Kirchoff's Rules
Sometimes the circuit is too complicated to reduce to a single resistor, especially if
there is more than one battery in the circuit. Then we use a set of rules, called Kirchoff's Rules, for determining the current through a circuit.
Junction Rule. The sum of the magnitudes of the currents directed into a junction equals the sum of the magnitudes of the currents directed out of the junction. (Conservation of charge) Loop Rule. Around any closed loop, the sum of the potential drops equals the sum of the potential rises. (Conservation of energy)
How to:
Draw the circuit and draw currents with an arrow in every separate branch of the circuit. A branch is a section where the current does not change. Apply the junction rule to enough junctions so that every current is used at least once. Apply the loop rule to enough closed loops so that each current appears at least once. Remember the sign convention for the potential changes:
Going across an "emf" is a plus sign if going from negative to positive and a
minus sign if going from positive to negative. (Plus if going in "normal" direction of current.) Going across a resistor is a plus sign if going against the current and a minus sign if going with the current. (Minus if going in "normal" direction of current.)
 |
 |
|
PROBLEM: Find the current and power in the 3W resistor in the circuit below using Kirchoff's Rules. Make sure to specify direction of current. What is the current in the other two resistors?
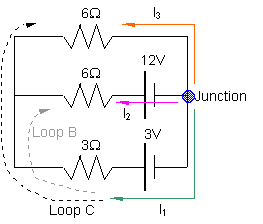 Apply the Junction Rule: Apply the Junction Rule:
I1 + I2 + I3 = 0
Apply the Loop Rule:
Loop (B)
3 - 3I1+ 6I2 - 12 = 0
ÞI2 = (1/2)I1 + 3/2
Loop (C)
3 -3I1 + 6I3 = 0
ÞI3 =(1/2)I1 - 1/2
Plugging equations (B) and (C) into (A)
I1 + (1/2)I1 + (3/2) + (1/2)I1 - 1/2 = 0
2I1 = -1 A ÞI1 = -1/2 A
I1= 1/2 A from left to right
P1 = I12R1= (-1/2 A) 2(3 W) = 3/4 W
From (B)
I2 = (1/2)I1 + 3/2 = -1/4 + 3/2 = 5/4 A right to left
From (C)
I3 =I1 - 1/2 = -1/4 - 1/2 = -3/4 A = 3/4 A left to right
|
|
|
Terminal Voltage
A real battery has some internal resistance. So if I were to draw a real battery it would
consist of a perfect battery and a resistor. I can treat this just like two separate components when I use Kirchoff's Laws or equivalent resistance. However, when I hook up
to the battery I do not quite get the entire potential from the battery. Instead I get something slightly smaller.
 |
 |
|
PROBLEM An ideal battery has a voltage of 9.0 volts and an internal resistance of 0.5 W. When it is drawing 0.3 amps, what is the terminal voltage?
VTerminal =Vo - Ir = 9.0 V - (0.3 A)(0.5 W) = 8.9 V
|
|
|
Capacitors in a Circuit
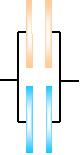 Parallel Parallel
When capacitors are in parallel, the total charge is the sum of the charge on each one, so...
Q = Q1+Q2 = C1V + C2V = V(C1 + C2) = CPV
so CP = C1 + C2 + ...
U = 1/2 CPV2
Series
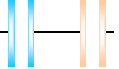 When capacitors are in series, the charge on each one is the same, so... When capacitors are in series, the charge on each one is the same, so...
V=Q/C1+ Q/C2 = Q(1/C1 + 1/C2) = QCs
so 1/ Cs = 1/C1 + 1/C2 + ...
So, equivalent circuits with capacitors are done the same as for resistors, except that they combine differently.
Resistors and Capacitors in a Circuit (RC circuit)
Attach a battery and the charge starts to build up. How fast?
Q = Qo[1-e-t/(RC)]
Since V = QC, this can also be written as V =Vo[1-e-t/(RC)] to determine the amount of
voltage on the capacitor at any time.
The value e is the natural logarithm. It is a transcendental number like p and it equals 2.718... It can be found on most scientific calculators. y=e-z.
RC=t is called the time constant. It is the time it takes for the capacitor to charge to 1/e of its total
charge, or about 63.2%.
The total charge on the capacitor is still given by qo=CV.
When discharging (draw circuit), we find
Q = Qoe-t/(RC) or in terms of voltage V = Voe-t/(RC)
and RC=t is the time it takes for the capacitor to lose 63.2% of its charge.
What if R is very small or 0, then e-t/(RC) is zero and the charging and discharging
happens instantaneously.
 |
 |
|
PROBLEM: How long does it take for 50% of the maximum charge to be deposited on this circuit
when the switch is closed. The resistor is 2 million ohms and each capacitor is 10 nF.
CS = 10´10-9 + 10´10-9 = 20´10-9 F
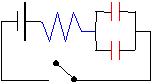 t = RC = (20 ´ 10-9 F)(2 ´ 106W) = 0.040 s t = RC = (20 ´ 10-9 F)(2 ´ 106W) = 0.040 s
q/qo = 0.50 = [1-e-t/(RC)]
e-t/(RC) = 1-0.5 = 0.5
ln(e-t/(RC) = -t/RC = ln(0.5) = -0.693
t = 0.693RC = 0.693(0.040 s) = 0.28 s
|
|
|
Electrical Safety and Grounding
 In a three-prong outlet, the third prong makes a path of less resistance from
the casing to the ground. Any current will flow through the third prong rather than through another body with more resistance. In a three-prong outlet, the third prong makes a path of less resistance from
the casing to the ground. Any current will flow through the third prong rather than through another body with more resistance.
|