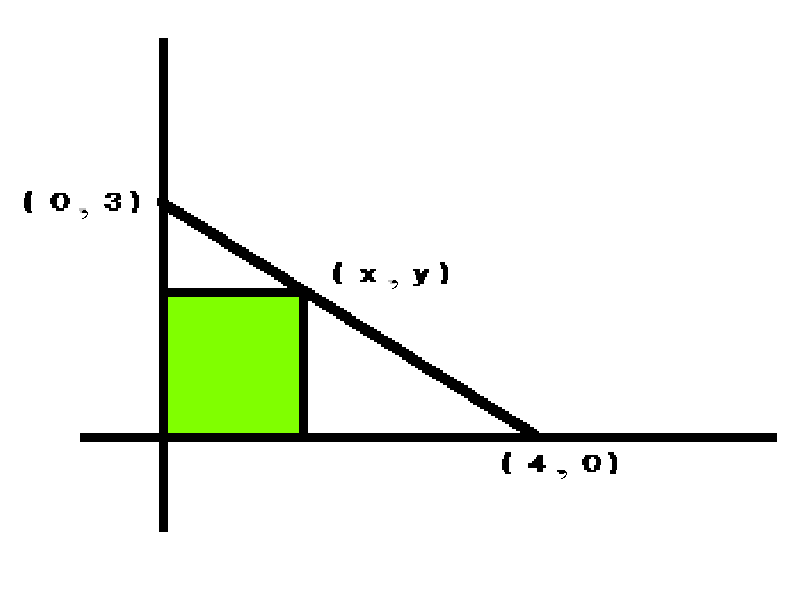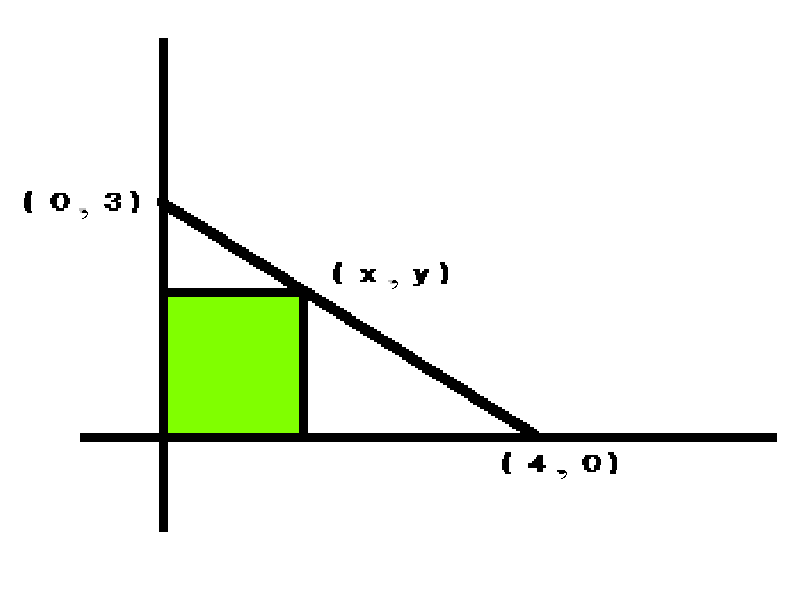- The student government wishes to build a rectangular recreation hall on the shore of Lake Fred. They wish to have the wall facing the lake made of glass and the other three walls made of brick. The cost per square foot of the glass is three times that of the brick. They need the floor area to be 200 square feet. What dimensions will minimize cost? (Ignore the thickness and height of the walls.)
- Bill got a summer job in a canning company. They want him to design a new cylindrical can to hold 100 cubic inches. If the cost of the material for the top and bottom is 2 cents per square inch and the cost of the material for the sides is 5 cents per square inch, what size and shape will minimize cost?
- An orange grove containing 60 trees per acre yields an average of 500 oranges per tree. For each additional tree per acre the yield per tree drops by 5 oranges. How many trees should be planted for maximum yield per acre?
- A manufacturer wants to make wooden crates with square bases and no top, of capacity 4 cubic feet. Find the dimensions that minimize the amount of wood used.
- A closed tin can is to be made in the shape of a right circular cylinder. If the cost of the material for the top and bottom is twice that of the material for the sides, find the dimensions, radius and height, that will minimize cost.
- Find the dimensions of the right circular cylinder of maximum volume that will fit inside a sphere of radius 2.
- A farmer wants to make a rectangular pen for his chickens using the side of his barn for one side of the pen and 100 ft of chicken wire for the other three sides. What dimensions will give him the pen of maximum area?
- Find two numbers whose product is -12 and the sum of whose squares is minimum.
- A farmer wishes to fence off two rectangular pens, each with 900 square feet of area, by making one large pen and then dividing it with a fence down the middle. What dimensions will require the least amount of material?
- A farmer wants to enclose 40,000 square feet along a roadside with two rectangular pens of the same size by fencing off one rectangular area then subdividing it with a fence perpendicular to the road. The fencing along the roadway costs $15 a foot, the fencing on the other three exterior sides costs $10 a foot and the fencing for the divider costs $5 a foot. What dimensions will minimize cost?
- Pam must design a right circular cylindrical can to hold pi cubic inches of tuna fish. The cost of the material for the top and bottom is 1 cent per square inch. The cost of the material for the sides is 2 cents per square inch. Assuming no waste, what dimensions will minimize cost? [remember: circumference of a circle is 2 pi r area is pi r squared]
- A wire 60 inches long is cut into two pieces. One of the pieces will be bent into an equilateral triangle and the other into a circle. Where should the wire be cut so that the area is a. a maximum? b. a minimum?
- Use the fact that 12 fluid ounces is approximately 21.66 cubic inches to find the dimensions of a 12-ounce soda can that can be constructed using the least amount of metal. Compare your answer to my soda can, what accounts for the difference?
- A right circular cone is to be inscribed in a sphere. Find the radius and height of the cone of maximum volume that can be so inscribed.
- Find the coordinates, (x,y) of the point which maximizes the area of the rectangle in the figure below.
Answers?
Selected solutions