MATH 230-001 Course Objectives
Spring Semester 2008
The "Mathematics Learning Cube"
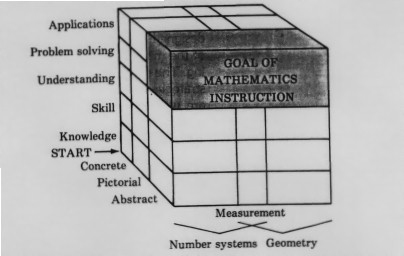
Here are objectives for students to consider in preparing for tests and the final exam.
1.1.1 Outline the four-step problem solving process
developed by George Polya. Briefly describe each
step.
(p. 4)
1.1.2 List five problem solving strategies. (See Sections 1.1, 1.2)
1.1.3 Given a problem, illustrate the use of Polya's problem solving steps in trying to solve the
problem.
(Exercises 1.1: 1, 3, 5, 7, 9, 13, 17, 21, 25)
1.2.1 Demonstrate the ability to identify arithmetic and
geometric sequences and the ability to apply the
method of
finite differences in solving problems. (Exercises 1.2: 12, 26, 28-34
all)
2.2.1 Given a table of data pairs, represent the data graphically. (Exercises 2.2: 3, 4)
2.2.2 Given a graph of a relationship, interpret the
pattern of change represented in the graph
and
translate from the graphical representation to the symbolic form.
(Express the
relationship
with a rule for a function.) (Exercises 2.2: 2, 11, 23-28)
2.2.3 Correctly
utilize tables, functional notation, and graphical representations in writing
up
problem
solutions. (Exercises 2.2: 15, 21)
6.1.1 Show how to use decimal squares to compare the numbers represented by two decimals.
(Exercises 6.1: 37)
6.1.2 Given a rational number expressed as a common fraction, calculate the decimal representation
for that number, and conversely given a terminating or repeating decimal determine the common
fraction representation for the number. (Exercises 6.1: 23, 24, 25, 26, 39)
6.2.1 Demonstrate how to use decimal squares to illustrate computations with decimals.
(Exercises 6.2: 3, 4)
6.3.1 Demonstrate the ability to convert among percents, decimals, and fractions. (Exercises 6.3: 2-11 odd)
6.3.2 Demonstrate the use
of ratios, proportions, percents, and scientific notation in solving problems.
(Exercises 6.3:
11-25 odd, 29-43 odd)
6.3.3 Demonstrate understanding of the concepts: percent
increase, percent decrease,
percent
change, percent greater, and percent less.
6.4.1 Explain what we mean by an irrational number.
6.4.2 Given a pair of rational numbers, name two
irrational numbers between the two
rational
numbers. (e.g. 7 and 8)
6.4.3 Given a pair or irrational numbers, name two
rational numbers between the two
irrational
numbers. (e.g. pi and the square root of 15)
6.4.4 Correctly classify numbers as rational or irrational. (Exercises 6.4: 1, 13)
6.4.5 Perform calculations on rational and irrational numbers. (Exercises 6.4: 3-9 odd, 15, 33, 35)
6.* Respond correctly to items like 9-20 on the "Chapter Test" on pp. 422-423.
Return to the top of this page.9.1.1 Demonstrate knowledge and understanding of the
following geometric entities, relationships, and
concepts: point, line, plane, space, collinear points, coplanar points,
between, line segment, half-line,
ray, perpendicular
lines, concurrent lines, parallel lines, skew lines, angle, half-plane, angle
measure,
segment
measure, acute angle, right angle, obtuse angle, straight angle, reflex angle,
adjacent angles,
complementary angles, supplementary angles, curve, convex set, polygon, and
diagonal.
(Exercises
9.1: 3-15 all, 22, 23, 28)
9.1.2 Given geometric figures, classify each one
of them as belonging to one or more of the following
categories: curve, simple curve, closed curve, simple closed curve,
polygon, convex polygon.
(Exercises 9.1: 17-20 all)
9.1.3 Classify triangles using the following
categories: scalene, isosceles, equilateral, right, obtuse, acute.
(Page
564, Example I)
9.1.4 Demonstrate knowledge of the following special
segments in triangles and some properties of
those
segments: angle bisector, median, altitude, perpendicular bisector of a
side. (Recall the
paper
folding activities we did in class.)
9.1.5 Classify quadrilaterals using the following
categories: trapezoid, parallelogram, rhombus,
rectangle,
and square. (See pages 563 and 564)
9.1.6 Define and illustrate the following terms:
circle, center, radius, diameter, chord, tangent, arc.
(See pages
562-563)
9.1.7 Given a geometric concept, design a creature card to
introduce that concept to children.
(e.g. curve, simple curve, closed curve, simple closed curve,
polygon, convex polygon,
collinear
points, concurrent lines, skew lines, parallel lines, adjacent angle, interior
angle,
exterior
angle)
9.2.1 Demonstrate knowledge of properties of the angles,
sides, and diagonals of polygons.
(Exercises
9.2: 2, 6, 7, 10, 11, 12, 16, 26)
9.3.1 Identify the five regular polyhedrons by name and for each type specify its number of faces
edges, and vertices.
9.3.2 Write Euler’s formula for the relationship between the number of faces, edges, and vertices
for any polyhedron.
9.3.3 Show how to use Euler’s formula to help you determine the number of faces, edges, and vertices
for a polyhedron.
9.3.4 Identify polyhedrons, cones, and cylinders by name. (Exercises 9.3: 8, 9)
9.4.1 Given a plane figure, identify any lines of symmetry for the figure.
9.4.2 Given a plane figure find and describe all its reflection and rotation symmetries.
(Exercises 9.4: 13, 14)
9.4.3 Given a sketch of a curve and a line, complete the sketch so that it is symmetric about the
given line. (Exercises 9.4: 17, 18)
.
9.* Respond correctly to items like 1-7, and 16-18 in the "Chapter Test" on pp. 623-625.
10.1.1 Given a description or picture of an object,
estimate its length in appropriate metric units
and US or English customary units. (Exercises 10.1: 3-14, 18, 19)
10.1.2 Given a description or picture of an object, estimate
its area in appropriate metric units
and US or English customary units.
10.1.3 Given a description or picture of an object,
estimate its volume or capacity in appropriate
metric units and US or English customary units. (Exercises 10.1:
3-14, 18)
10.1.4 Given a description or picture of an object,
estimate its mass in appropriate metric units
and US or English customary units. (Exercises 10.1: 3-14, 19)
10.1.5 Given a description of an environment, estimate the
temperature in the environment in
appropriate Celsius units and Fahrenheit units. (Exercises 10.1:
20)
10.1.6 Explain how we distinguish between the meanings of
accuracy and precision of measurement.
(e.g. Suppose a student measured two objects and said their lengths were
6 cm and 60 cm
respectively. Which measurement is more precise, or are they of equal
precision? Explain
your answer. Comment on the accuracy of the student's measurements.)
10.1.7 Determine the greatest possible error and the
relative error of a measurement.
(Find the greatest possible error and the relative error for the two
measurements of
Objective 10.1.6 above.) (Exercises 10.1: 23)
10.1.8 Demonstrate the ability to convert from metric to
US or English customary measurements
and conversely from US or customary measurements to metric measurements.
(Exercises 10.1: 15, 22)
10.1.9 Given information concerning the time required to travel a particular distance, determine the
average rate of speed in specified units. (e.g. If one walks 110 yards in one minute, what is
his or her average rate of walking in kilometers per hour?)
10.2.1 Given a
description or picture of a polygon, circle or other plane figure, find its
perimeter
and area using non-standard and appropriate metric or US or English customary units.
(Exercises 10.2: 2, 3, 6-21 all)
10.2.2 Solve problems using length, angle, area, and perimeter relationships. (Exercises 10.2: 23, 24, 31-35)
10.3.1 Demonstrate the ability to determine both the
volume and surface area of solid figures such as
pyramids, prisms, spheres, cylinders, and cones. (Exercises 10.3:
7-14)
10.3.2 Solve problems involving surface areas and volumes. (Exercises 10.3: 15-29 odd)
10.* Respond correctly to items like those on the "Chapter Test" on pp. 703-705.
M.1 Represent and analyze relationships using tables,
graphs, verbal rules, and equations.
(See also
objectives for Section 2.2 in the Bennett & Nelson text.)
M.2 Given data in a sequence identify patterns and specify
rules for generating the sequence
in the form of
difference equations and functional equations. (See also the objectives
for Section 1.2 in
the Bennett & Nelson text.)
Link to a summary of three kinds of growth. Link to some examples.
M.3 Translate among tabular, graphical, symbolic, and rule
(both difference equations and
explicit
functional) representations of functions. (See also objectives for
Section 2.2
in the Bennett
& Nelson text.) Link to
some sample exercises.
M.4 Use curve fitting to predict from data.
(Bennett & Nelson,
Fifth Ed. Exercises 7.2: 35-38; Sixth Ed. Exercises 7.1: 35-38)
M.5. Given a set of data pairs, fit an appropriate function
(curve) to the data, comment on
the goodness of
your fit, and make predictions using your function.
M.6 Use graphical, numerical, and theoretical methods with
mathematical models to make
conclusions and
predictions.
M.7 Use sequences and difference equations to express patterns in data.
M.8 Translate among tables, graphs, difference equations
and functional equations in
solving problems.
M.9 Employ the concepts of change (growth), average rate of change
(growth), and
percent change (growth)
in analyzing data, looking for patterns, and fitting models to data.
M.10 Employ the concepts of change (growth), average rate
of change (growth), and percent
change
(growth) in analyzing data, looking for patterns, and fitting linear,
quadratic, and
exponential
functions to data.
(Link to some examples.)