|
 Chapter 11 Lecture Notes Chapter 11 Lecture Notes
Formulas:
Demonstrations:
- Mass on a spring.
- Pendulum of two masses.
- Forced vibrations with springs and pendulum.
- Transverse and Longitudinal Waves.
Main Ideas:
-
 Simple Harmonic Motion Simple Harmonic Motion
- Energy Description
- Kinematic Description
- Relationship with Circular Motion
- Applied to a Pendulum
- Other Periodic Motion
- Damped Motion
- · Forced Vibrations and Resonance
- Wave Motion
- Types of Waves
- Description of Waves
- Superposition and Reflection
- Standing Waves, Resonant Frequencies
- Refraction and Diffraction
Simple Harmonic Motion
Vibrations and waves are an important part of life. Every sound you hear is a result of
something first vibrating, then a sound wave traveling through the air as the air molecules vibrate, then your eardrum vibrating and the brain interpreting that as sound. The simplest
vibrational motion to understand is called simple harmonic motion (SHM). SHM occurs
when I move an object from its equilibrium position and the force that tries to restore the object back to its equilibrium position is equal to the distance from the equilibrium position. In other words,
F = -kx.
This is exactly Hooke's Law for springs. So ideal springs exhibit SHM. The motion of the object at the end of a spring repeats itself after a period of time. It is periodic with a
period T, the amount of time it takes to complete one cycle. The frequency is the number of cycles per unit time, so
f = 1/T.
The frequency is measured in cycles/second. 1 cycle/second = 1 Hertz (Hz). The maximum distance from the equilibrium point is called the amplitude (A), and the distance
from the equilibrium point at any time is the displacement.
 |
 |
|
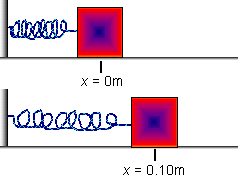 PROBLEM: A 0.35-kg mass attached to a
spring with spring constant 130N/m is free to move on a frictionless horizontal surface. If the mass is released from rest at x=0.10m,
find the force on it and its acceleration at (a) x=0.10m, (b) x=0.050m, (c) x=0m, and (d) x=-0.050m PROBLEM: A 0.35-kg mass attached to a
spring with spring constant 130N/m is free to move on a frictionless horizontal surface. If the mass is released from rest at x=0.10m,
find the force on it and its acceleration at (a) x=0.10m, (b) x=0.050m, (c) x=0m, and (d) x=-0.050m
F = -kx = -kA
F = -(130N/m)(0.10m)= -13 N
a = F/m = -13 N/.35 kg = -37 m/s2
This is the maximum force and maximum acceleration in the period.
F = -kx = -(130 N/m)(0.050 m) = -6.5 N
a = F/m = -6.5 N/.35 kg = -19 m/s2
Note that the acceleration for an object moving with simple harmonic motion is not constant since F is not constant.
F = -kx = -(130 N/m)(0.00 m) = 0 N
a = F/m = 0 N/.35 kg = 0 m/s2
When the spring is un-stretched, the force and acceleration are zero (but the velocity is at its maximum).
F = -kx = -(130 N/m)(-0.050 m) = 6.5 N
a = F/m = 6.5 N/.35 kg = 19 m/s2
When the mass is on the negative side, the force and acceleration are positive.
|
|
|
Let's look at various aspects of simple harmonic motion including energy, motion, relationship with circular motion, and relationship with pendulum motion.
Energy of Simple Harmonic Motion
The simple harmonic oscillator is an example of conservation of mechanical energy. When the spring is stretched it has only potential energy U = (1/2)kx2 = (1/2)kA2 where A
is the maximum amplitude. When the spring is un-stretched, it has only kinetic energy K = (1/2)mv2 = (1/2)mvo2 where vo is the maximum velocity which occurs when the spring in
un-stretched. At any point in the motion of the object, it has a total energy equal to its potential energy plus its kinetic energy.
E = KE + PEelastic = KEmax = PEmax
E = (1/2)mv2 + (1/2)kx2 = (1/2)mvo2 = (1/2)kA2
 |
 |
|
PROBLEM: A
0.24-kg mass is attached to a horizontal spring that has a spring constant of 86 N/m. The spring is initially stretched to 0.23 m. If there is no friction so that the spring
oscillates with SHM how much energy is kinetic and potential when the spring is at (a) x = .10 m, (b) x = 0.0 m
(a) E = (1/2)kx2= (1/2)(86 N/m)(.23 m) 2= 2.3 J
(b) E = U + K = (1/2)kx2 + (1/2)mv2= 2.3 J
U =(1/2)kx2= (1/2)(86 N/m)(.1 m) 2= 0.43 J
K = E -U = 2.3 - .43 =1.9 J
(c) It is all kinetic at the midpoint, so K = 2.3 J
|
|
|
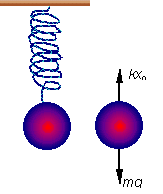 Let's suppose that the spring is not horizontal, but is instead in a vertical
position. The motion is basically the same as a horizontal spring except for where the equilibrium position is located. The equilibrium position is found by looking at all the forces on the mass. Let x0 be the new
equilibrium position. Let's suppose that the spring is not horizontal, but is instead in a vertical
position. The motion is basically the same as a horizontal spring except for where the equilibrium position is located. The equilibrium position is found by looking at all the forces on the mass. Let x0 be the new
equilibrium position.
kxo = mg Þ xo = mg/k
If you now move the spring an additional distance of x the forces on the mass are given by
F = -k(xo + x) + mg = -k(mg/k + x) + mg = -kx,
so even a vertical spring behaves as if it was horizontal with the restoring force equal to -kx. Also, the energy of compressing a vertical spring is the same as a horizontal
spring. So a vertical spring acts exactly like a horizontal spring only the equilibrium position is displaced due to gravity.
Kinematics of Simple Harmonic Motion
So how does a simple harmonic oscillator move? We have seen that when the spring
is displaced by its maximum amount in a particular situation, then the potential energy is a maximum and the kinetic energy (velocity) is zero. When the spring is at its equilibrium
position after being displaced, then it has a maximum velocity and, therefore, a maximum kinetic energy. If I use the energy equations from above to solve for velocity, I get,
(1/2)mv2 + (1/2)kx2 = (1/2)kA2
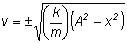
And if I set the maximum kinetic energy equal to the maximum potential energy, I get (1/2)mvo2= (1/2)kA2Þ
vo2= (k/m)A2
so plugging this into the above equation gives
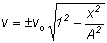
This tells the velocity at any position as a function of the maximum velocity and of the
maximum displacement (amplitude). Look at what it says. When the position is the same as the amplitude (x =A), the velocity is zero. When the position is the equilibrium position (x =0), the velocity is a maximum (vo).
Relationship of SHM to Circular Motion
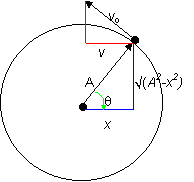 Consider an object rotating around in a circle. If I look at one point of that object from the side I will see that the
object appears to be following simple harmonic motion. We will look at the projection of the motion along the x-axis. (See figure 11-6 in the book). The object always has a
speed of vo. However, the x component of the velocity, the part of the velocity which is viewed from our observer changes. Because the triangles are similar (all three angles are the same), Consider an object rotating around in a circle. If I look at one point of that object from the side I will see that the
object appears to be following simple harmonic motion. We will look at the projection of the motion along the x-axis. (See figure 11-6 in the book). The object always has a
speed of vo. However, the x component of the velocity, the part of the velocity which is viewed from our observer changes. Because the triangles are similar (all three angles are the same),
sinq = v/vo
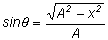
We can put these equations together.
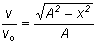
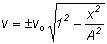
which is the equation for a simple harmonic oscillator. (If the equations are the same,
then the motion is the same). Since we have already dealt with uniform circular motion, it is sometimes easier to understand SHM using this idea of a reference circle. For
instance, the speed of the ball going around the circle is given by distance divided by time.
vo = (2pA)/T or T = (2pA)/vo
where T is the period and A is the amplitude and v0 is the maximum velocity. If I now use vo2= (k/m)A2, I get
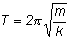 or for the frequency, I get or for the frequency, I get
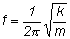 . .
So we see that frequency does not depend on amplitude, but it does depend on the spring constant and the mass.
If we know the location of the mass and the amplitude of the oscillation, then we know the velocity from
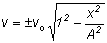 . But suppose I wanted to know the location as a function of
the time. Where will the mass be after 1 second, or after 100 seconds? From our figure, we see that . But suppose I wanted to know the location as a function of
the time. Where will the mass be after 1 second, or after 100 seconds? From our figure, we see that
x = Acosq,
and since the mass is rotating with angular velocity w, we see that q = wt, and from w = 2pf = 2p/T, we get,
x = Acoswt = Acos(2pft) = Acos(2pt/T).
Now we see that the motion is periodic. After a time where t= T, we get the mass is at a position of cos(2p) = cos(0) = cos(2np) where n is any integer. The mass keeps coming back to
the same position. The motion is also sinusoidal as a function of time. That is if I plot position versus time, I will get a sine (or cosine) curve.Similarly, the velocity is sinusoidal.
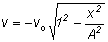
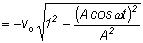
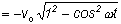
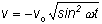 = -vosinwt = -wAsinwt = -vosinwt = -wAsinwt
(sincevo = wA)
v = -wAsinwt
and the acceleration is sinusoidal. We can see this from Newton's second law.
a = F/m = -kx/m = -(kA/m)coswt = (vo2/A)coswt = w2Acoswt
a = w2Acoswt
To use these, keep in mind that vo = wA, and vo2= (k/m)A2
Whether it is a sine or cosine function for x and acceleration just depends on whether
the mass starts at the equilibrium position or at the maximum. Displacement and acceleration are the same (sine or cosine), but velocity is the opposite. We say velocity is "out of phase" with displacement.
 |
 |
|
PROBLEM: Suppose I have a spring that oscillates according to the following equation. What is the
amplitude, the frequency, and the period of the oscillation?
x = (0.25 m)cos(pt/8.0)
We compare this with the equation for position and see that,
Amplitude = 0.25 m.
pt/8.0 = 2pft Þ 1/8.0 = 2f Þf = 1/16 Hz
T = 1/f = 16 s.
|
|
|
SHM and Simple Pendulums
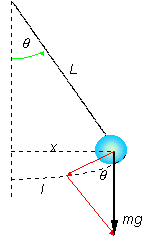 A simple pendulum acts like a harmonic oscillator if the displacement is small. We can see this
from looking at the forces on a pendulum. A simple pendulum acts like a harmonic oscillator if the displacement is small. We can see this
from looking at the forces on a pendulum.
F = -mg sinq
To be a simple harmonic oscillator, the force must be proportional to the distance the pendulum bob has moved.
Recall that the arclength (l) is given by
q = l /L in radians, and that sinq = x/L from the figure. Now if the angle is small, then x»l and q = sinq = x/L, or
F = -mgq =-mgx/L
which looks just like F = -kx if k = mg/L .
So for small angles, a pendulum acts like a simple harmonic oscillator with a spring constant of mg/L. (Remember if the equations are the same then the motion is the
same). The period is given by
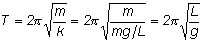
So the period or frequency does not depend on the mass of the pendulum, only its length.
Demonstration: Pendulum of two masses.
 |
 |
|
 PROBLEM: A man wants to know the height of a building
which has a pendulum hanging from its ceiling. He notices that in one minute the pendulum oscillates 8 times. What is the height of the building? PROBLEM: A man wants to know the height of a building
which has a pendulum hanging from its ceiling. He notices that in one minute the pendulum oscillates 8 times. What is the height of the building?
f = 8 revs/60 seconds = 0.13 s-1, so
f = (1/2p)Ö{g/L}
L = g/(4p2f2) = (9.8 m/s2)/{(4p2(0.13s-1)2}
L = 14.7 m
If the length were cut in half, what would the new frequency be?
f = (1/2p)Ö{g/L}, so if L changes to L/2, frequency changes to fÖ2
f = .13Ö2 = 0.19 s-1.
|
|
|
Other Periodic Motion
Damped Oscillations
Most oscillations do not continue on forever, but eventually stop, due to some kind of
non-conservative force like friction or air resistance. Some vibrations are purposely stopped. Your shock absorbers in your car are made to stop the vibrations set up by the
road. All these vibrations, which are eventually stopped, are called damped vibrations, or if the harmonic motion is stopped, it is called damped harmonic motion. When the motion
is damped, mechanical energy is not conserved.
Driven Oscillations
The opposite of damped vibrations are vibrations that are driven or forced. I can drive
it at any frequency, but if I drive it at its natural frequency, then its amplitude rises without any limits.
 |
 |
|
PROBLEM: I have a spring that requires 4 N to stretch .1 m, so
k = F/x = 4/.1 = 40 N/m.
If I hang a 1 kg mass from the spring, it should have a natural resonant period of:
T = 2pÖ{m/k} = 0.99 s, or almost exactly 1 second.
So if I push on the spring with any other period, I force oscillations, but if I push with that period, the amplitude continues to
increase.
For a pendulum with a length of .84 meter,
T = 2pÖ{L/g} = 1.84 s
If I push every 1.84 seconds, I will hit the resonant frequency, and the amplitude will increase dramatically.
|
|
|
Everything has a natural frequency, like musical instruments, children's swings and
bridges. Foot soldiers don't march in step across a bridge, so that they won't accidentally set up a resonance in the bridge and it oscillates and collapses. Oscillating air at the
resonant frequency of a glass is what causes it to shatter.
Wave Motion
 Oscillations can cause waves. So it is natural to use the
concepts and terminology developed in our discussion of harmonic motion to begin to talk about waves. The world is full of waves: sound waves, waves on a string, earthquake waves,
and electromagnetic waves. Waves are oscillations that carry energy from one place to another, yet matter is not carried with the wave. Setting up dominoes and knocking them down
illustrates this. Each domino moves very little, but the energy may move over a long distance. If you watch a leaf or a cork on a lake as waves move by it, the leaf or cork moves very little, but
the wave moves a long ways. Waves may move in one, two or three dimensions. A wave pulse on a rope basically moves in one dimension. Water waves on a lake move in two dimensions, and spoken
sound waves spread out in three dimensions. In this chapter we will talk about waves that require some kind of medium to travel in, like sound waves, earthquake waves, and waves on a string. Next
semester we will talk about electromagnetic waves, which do not require any medium to travel in. We will find that there are many similarities in all wave motion. Oscillations can cause waves. So it is natural to use the
concepts and terminology developed in our discussion of harmonic motion to begin to talk about waves. The world is full of waves: sound waves, waves on a string, earthquake waves,
and electromagnetic waves. Waves are oscillations that carry energy from one place to another, yet matter is not carried with the wave. Setting up dominoes and knocking them down
illustrates this. Each domino moves very little, but the energy may move over a long distance. If you watch a leaf or a cork on a lake as waves move by it, the leaf or cork moves very little, but
the wave moves a long ways. Waves may move in one, two or three dimensions. A wave pulse on a rope basically moves in one dimension. Water waves on a lake move in two dimensions, and spoken
sound waves spread out in three dimensions. In this chapter we will talk about waves that require some kind of medium to travel in, like sound waves, earthquake waves, and waves on a string. Next
semester we will talk about electromagnetic waves, which do not require any medium to travel in. We will find that there are many similarities in all wave motion.
Types of Waves
There are two basic types of waves: transverse waves and longitudinal waves. Each type of wave describes the motion of a small segment of the wave. In a
transverse wave, each segment moves perpendicular or transverse to the direction of motion of the wave. This is like a rope with a pulse on it. In a longitudinal wave, each
segment moves along the direction of the the motion of the wave. This is like a spring or slinky which is quickly compressed, then returned to its original position.
Demonstration: Transverse and Longitudinal Waves.
Description of Waves
The shape of a wave on a string gives a good picture of a wave. The maximum height of the wave is called the amplitude. The distance from one point on the wave to the
same point on the next wave (like crest to crest, or trough to trough) is one wavelength, denoted by the Greek letter lambda (l). The speed with which the wave moves is called the wave velocity
(v). That is, what is the distance an individual crest travels in a certain amount of time. The wave velocity is not the velocity of the individual segments of the wave (a part of the rope or a
single domino). It is the velocity that the wave, as a whole, moves. If I stay at one location and count the number of waves that go by in a given amount of time - that is called the frequency.
The period is the time it takes for one complete oscillation of the wave. Since velocity is distance divided by time, we see that the wave velocity is given by
v = l /T =lf
The speed of a wave in a certain medium is determined by the properties of the medium.
We find that for a stretched string the speed with which the wave moves is given by
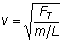
where FT is the tension in the rope, L is the length of the rope, and m is the mass of the rope. The quantity m= L/m is called the linear density of the rope.
Sound travels by creating longitudinal waves in the air. Some kind of medium is
required for sound waves to be created. In the vacuum of space, sound waves do not travel, and no one can hear you scream. In general, the velocity of a longitudinal wave traveling in a liquid is given by
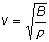
where B is the bulk modulus (see table 9-1, page 240) and r is the density of the material.
The density is defined as the mass per unit volume (r=m/V, kg/m3) and many values of densities for
various materials are given in the textbook. This equation also works approximately (though not precisely) for a gas.
 |
 |
|
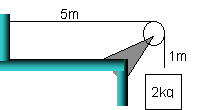 PROBLEM: A string has a mass of 0.300 kg
and a length of 6.00 m and is set up as shown in the picture at the right. What is the speed of a
pulse on this string? PROBLEM: A string has a mass of 0.300 kg
and a length of 6.00 m and is set up as shown in the picture at the right. What is the speed of a
pulse on this string?
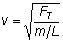
v = Ö{(2 kg)(9.8 m/s2)/(0.300 kg/6 m)} = 19.8 m/s
|
|
|
 |
 |
|
PROBLEM: How fast does sound travel in air, and in water?
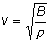
In air: v = Ö{1.01´105 N/m2/1.29 kg/m3} = 280 m/s
(The actual value for air is more like 340 m/s and depends on the temperature of the air.)
In water: v = Ö{2.0´109 N/m2/1.0´103 kg/m3} = 1.4´103 m/s
|
|
|
Superposition and Reflection
An important aspect of waves is the principle of the superposition of waves. This principle states,
If two or more traveling waves are moving through a medium, the resultant
wave is found by adding together the displacements of the individual waves point by point.
So if there are two waves approaching each other on the same string, they will interfere
with each other. If they both have a positive amplitude, they will interfere constructively, and the resultant wave will have a larger amplitude. If one wave has a positive amplitude and one has a negative amplitude, they will interfere destructively,and the resultant wave will have a smaller amplitude.
If the waves are moving in the same direction, then there will be constructive or
destructive interference only if the waves have the same wavelength. If the waves have their greatest positive amplitudes at the same point, we say that the waves are in phase and they demonstrate constructive interference. If one wave has its greatest positive
amplitude where the other wave has its greatest negative amplitude, we say the waves are out of phase and they demonstrate destructive interference.
One way of creating a wave traveling in the opposite direction is to have the wave
reflect off of an object. If a rope is attached to a wall and a pulse is generated on the rope, it will reflect when it reaches the end. If the rope is firmly attached the reflection will
actually invert the amplitude of the pulse. If the rope is attached with a ring (it is free to move), then the amplitude will not be inverted. If a thick rope is attached to a thin rope,
then part will be reflected and part will be transmitted.
Standing Waves, Resonant Frequencies
One of the most important concepts regarding waves is the concept of standing waves
and resonant frequencies. These ideas explain many aspects of sound including why different instruments, or different shaped volumes, create different sounds. A standing
wave is a wave in which every point on the wave oscillates with the same frequency, and each point has a maximum amplitude which does not change, (although every point may
have a different maximum amplitude). Any standing wave will have certain parts of the wave which do not move at all, and are called nodes
and other parts of the wave which have maximum movement and are called
anti-nodes. For any given geometric situation, a standing wave can only be created for certain frequencies, which are called natural frequencies or
resonant frequencies. A standing wave is really a set of waves moving
in opposite directions with the same velocities. That is why you can create standing waves by attaching a rope at one end and vibrating the other end. The waves are
reflected off of each end and the two waves interfere to produce a standing wave. This will only work if the rope is vibrated at the certain resonant frequencies. A standing wave
does appear to be standing in place, and a traveling wave does appear to be moving. Yet a standing wave is really the superposition of traveling waves moving in opposite directions.
If I have a rope that is tied down at each end and I want to set up standing waves in the
rope, I have a constraint. The constraint is that each end of the rope cannot move. So each end of the rope is a node. Then there are only certain ways I can set the rope
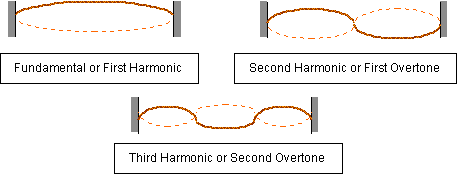
vibrating. These different ways are called harmonics. (See figure 11-33 in the book). If
the only nodes are at the end, we call this the first harmonic or it is also called the fundamentalfrequency or mode.
When I have one other node, this is called the second harmonic, or the first overtone, and when I have two more nodes we call it the third harmonic, or the
second overtone, and so forth. This is true not only for ropes, but also
for standing sound waves in an air column. So, harmonics of an instrument are determined by the length of the air column in the instrument. In fact, every object can be
set to vibrating at different harmonic frequencies and these frequencies are determined by the size and shape of the object.
 |
How do we determine the wavelength or frequency of the harmonics. We note that the
must be some fraction of the total length of the string (or air cavity for sound waves). For the first harmonic L = (1/2)l1. For the second harmonic, L =l2. For the third harmonic, (3/2)L =l3, and so on.
So in general
L = nln/2, or ln = 2L/n for the nth harmonic.
The standing wave is equivalent to two traveling waves moving in opposite directions, so
we can still calculate the velocity of the waves moving on the string. From the equations, v = l/T =lf, and
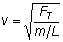 we find that we find that
fn = nv/(2L)
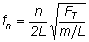
The last two equations are useful. Although you may need them on a test, they are not
necessarily on the equation sheet because they are easily derived from the more fundamental equations, ln = 2L/n,v = l/T =lf, and
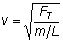 . You should know how to use these three equations in appropriate combinations. . You should know how to use these three equations in appropriate combinations.
What happens when you play a stringed instrument and you press down on the strings in a certain point? You are changing which harmonic oscillates.
The mass per unit length stays the same (m/L), and the tension stays the same so the
velocity of the traveling waves which make up the standing waves also stays the same since
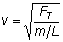 . However, the frequency and the wavelength change in such a way that v =lf. If the wavelength is reduced by a factor of 2, the frequency increases by a factor of 2, so that v stays the same. . However, the frequency and the wavelength change in such a way that v =lf. If the wavelength is reduced by a factor of 2, the frequency increases by a factor of 2, so that v stays the same.
 |
 |
|
 PROBLEM
: A violin string of length 33 cm is under a tension of 55
N. The fundamental frequency of the string is 196 Hz. (a) At what speed do the waves travel on the string? (b) What is the mass of the
string? (c) How far from one end of the string would you have to press the string in order that the remainder of the string have a fundamental frequency of 300 Hz? PROBLEM
: A violin string of length 33 cm is under a tension of 55
N. The fundamental frequency of the string is 196 Hz. (a) At what speed do the waves travel on the string? (b) What is the mass of the
string? (c) How far from one end of the string would you have to press the string in order that the remainder of the string have a fundamental frequency of 300 Hz?
(a)fn = nv/(2L). For the fundamental, n =1
v = 2L fn = 2(.33 m)(196 Hz) = 129 m/s
(b) FT= mv2/L
m =FTL/v2 = (55N)(.33m)/(129m/s)2
m = .00109 kg
m = 1.09 g
(c) Let's call the new position L¢ with a new
frequency f¢, and a new wavelength l¢. Then
l¢f ¢ = lf
2L¢f ¢ = 2Lf
L¢ = Lf/f ¢ = (.33 m)(196 Hz)/(300 Hz)
L¢ = .216 m
Note that the mass of the total string is 1.09 g, but the mass of the smaller part
vibrating is not 1.09 g. So to figure out the mass density (m/L) you must use the total length of .33 m. Then m/L = .00109kg/.33 m = .0033 kg/m .
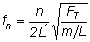
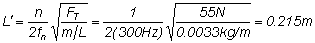 |
|
|
Here is a trick to solving these problems. Since
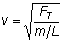 , then any string with a given tension and mass per unit length has the same velocity. So , then any string with a given tension and mass per unit length has the same velocity. So
v = fnln = 2fnL/n = 2fmL/m
or
fn/n = fm/m
where n is for one harmonic, and m is for another harmonic. If I set m = 1, I get
fn = nf1
This formula can be very useful for solving many problems.
 |
 |
|
PROBLEM: A string has its fundamental at 200 Hz. What is the difference in the frequency between
the first two overtones?
f2 = 2f1 = 2(200 Hz) = 400 Hz
f3 = 3f1 = 3(200 Hz) = 600 Hz, so the difference is 200 Hz.
|
|
|
Refraction and Diffraction
When a wave encounters an obstacle, they bend around the obstacle. This is called diffraction. The amount of bending depends on the size of the wavelength and the size
of the object. It is diffraction that allows us to hear sounds even when the source is not directly in line with us. For instance, if you go around a corner and talk, I can still here you
because the waves are bent around the obstacle, which is the wall. We will study diffractions quite a bit more next semester when we encounter electromagnetic waves.
When a wave travels from one medium to another, (like from air to water), part of the
wave is reflected and part continues into the medium and is transmitted. The part that is transmitted will often move in a different direction from the original wave. This phenomenon is called refraction. Refraction will particularly important when we discuss
light in the next semester. The wave is refracted because it changes velocity in the new medium. See figure 11-36 which shows how wave fronts will change direction if they
move at a different velocity. We find that the change of angle is related to the velocity of the wave in the different media, so sinq2/sinq1 = v2/v1 where q1 is the angle of incidence, q2
is the angle of refraction, v2 is the velocity in the medium of refraction and v1 is the velocity in the initial medium.
 |
 |
|
PROBLEM: A longitudinal earthquake wave strikes a boundary between two types of rock at a 25° angle. As it crosses the boundary, the specific gravity of the rock changes from 3.7 to 2.8. Assuming that the elastic modulus is the same for both types of rock, determine the angle of refraction.
The specific gravity is the ratio of the density of a substance to the density of water. We use the ratio of the sines.
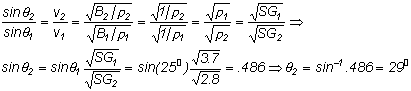 |
|
|
 Refraction and diffraction occur for all types of waves. They are very important concepts when
we talk about electromagnetic waves next semester. Refraction and diffraction occur for all types of waves. They are very important concepts when
we talk about electromagnetic waves next semester.
|