 |
|||||||
|
|
|||||||
|

Formulas: v» (331 + 0.60T ) m/s
ln= 2L/n, f = nv/2L n= 1,2,3,... for a tube open at both ends. ln= 4L/n, f = nv/4L n= 1,3,5,... for a tube open at only one end Demonstrations:
The Nature of Sound
SpeedThe speed of the sound wave will depend on the medium in which the sound is traveling. Since the approximate speed of sound is given by Ö{B/r}, the speed of sound will increase if the density is decreased, or if the bulk modulus is increased. Table 12-1 shows the speed of sound in various materials. If sound is traveling in a gas, its speed will depend on the temperature of the gas. For air which is at 0° C, (32°F), the speed of sound is 331 m/s. We can determine the approximate speed of sound in air at different temperatures from the equation v»(331 + 0.60T) m/s where T is the temperature in Celsius.
We use d = vt Pitch The pitch refers to whether the sound is a high or low note. High frequencies create high pitches and low frequencies produce low pitches. The human ear can hear frequencies between about 20Hz and 20,000Hz. These are audible sounds. Sound waves with frequencies above 20,000Hz are called ultrasonic. Dogs can hear sounds up to about 50,000Hz. So a whistle that only dogs can hear has a frequency higher than 20,000 but lower than 50,000Hz. Sound waves with frequencies below 20Hz are called infrasonic. IntensityThe intensity of the sound wave is a measure of how loud it is. The intensity is given by the power per unit are IºP/A. If there is a lot of power over a small area, then the sound wave is very intense. The intensity is given in Watts/meter2. For a sound to appear twice as loud to a human ear requires an intensity that is about 10 times greater. For this reason, intensity is measured on a log scale using the units of bel's or one tenth of a bel, a decibel. A decibel measures the sound level intensity or decibel level. (Look for the key word "level".) Whereas I is simply called the "intensity." A decibel is defined using the equation b= 10 log(I/Io) where Io is a the sound intensity at the lower threshold of hearing, taken to be Io = 1.0 ´10-12 W/m2 and log is the base 10 logarithm. The intensity of various sounds is given in Table 12-2. Recall that power is defined as energy per unit time. P = E/t. For a wave the energy is proportional to the square of the maximum amplitude. Eµxo2. So the intensity of a sound wave, or its loudness, is proportional to the square of amplitude. We see that different aspects of the wave determine different audible characteristics. The pitch is determined by the frequency of the wave and loudness is determined by the maximum amplitude of the wave. PROBLEM: What is the intensity level of a sound wave having an intensity of (a) 1.0 ´ 10-12W/m2, (b) 1.0 ´ 10-11 W/m2 and (c) 1.0 ´ 10-10W/m2 (a) b= 10 log(1.0 ´10-12 W/m2/1.0 ´ 10-12 W/m2) = 0 db Note that an increase from 0 to 10 db corresponds to an intensity which is ten times greater. An increase from 0 to 20 db corresponds to an intensity which is 100 times greater. So a 100 db sound is 1000 times more intense than a 70 db sound. (The difference is 30 db). See appendix A for a review of logarithms.
30 db = 10 log(I/1.0 ´10-12 W/m2) The intensity is cut in half, so it now becomes 0.5´10-9and the new decibel level is, b= 10 log(0.5 ´ 10-9W/m2/1.0 ´10-12 W/m2) = 27 db. So a decrease in sound intensity by a factor of two only decreases the intensity level by 3 db. The most sensitive ears can hear a change in intensity level of only 1 or 2 db. Spherical WavesMost sound waves travel out in all directions from a source. Since the intensity is equal to the Power/Area, what happens as the sound spreads out? The total power stays the same, but it is spread out over an increasingly large spherical area. Since the area of a sphere is given by 4pr2, the intensity goes as P/4pr2, where r is the distance the listener is from the source of the sound. So I = P/4pr2
PROBLEM: During a fireworks show a rocket explodes. To a listener who is 640 m away, the sound has an intensity of 0.10 W/m2. What is the intensity for a listener who is 160 m away? P = I4pr2 Since the power is the original power of the rocket explosion, that is the same for both listeners. I24pr22 = I14pr12 Sources of SoundSound is produced when an object vibrates. Almost any object can vibrate and produce a sound. Musical instruments tend to make use of vibrating strings or of vibrating columns of air to produce pitches that are certain frequencies. Frequencies for notes (in music from the western world) are on the equally tempered chromatic scale. (See Table 12-3). Strings
v = l /T = lf (velocity of a wave related to its wavelength and frequency)
l= v/f = 2L/n. These are fundamental so n=1 When we push the string on the fret down, the tension and linear mass density remain the same, so the velocity is the same. TubesMany instruments use standing waves produced in vibrating columns of air to create notes. The most important point in understanding this is to realize that if an air cavity is closed, then the air cannot move against the wall, so a node is created at the wall. Let's look at air cavities open at both ends, then at cavities closed at one end. (See Figure 12-12 in the book).
First Harmonic L = (1/2)l, f = v/2L
Second Harmonic L = l,f = v/L
In general ln= 2L/n, f = nv/2L n = 1,2,3,... for a tube open at both ends. If we have an open tube then the frequency is determined by the velocity of the wave in the tube (which is determined by what the material is in the tube), by the length of the tube, and by which of the harmonics (n) is formed. When you inhale Helium, you change the velocity of the air in you throat cavities, thus changing the frequency, and the pitch of your voice. For tubes that are closed at one end, the air next to that end cannot move, so there will always be a node at that end and an anti-node at the other. The anti-node is at the other because the air will always move at the open ends of the tube.
First Harmonic L = (1/4)l, f = v/4L
Third Harmonic L = (3/4)l, f =3v/4L
In general ln= 4L/n, f = nv/4L n = 1,3,5,... for a tube open at only one end. Note that for the tube open at only one end, only odd harmonics can be formed since one end must be a node.
PROBLEM: A flute with all of the holes closed can be considered as a tube with both ends open. It has a fundamental frequency of 261.6 Hz (which is middle C). If the air temperature is 20°C, how long is the flute? At 20° C, the velocity of air is 343 m/s. So f = nv/2L. PROBLEM: A particular organ pipe can resonate at 264 Hz, 440 Hz, and 616 Hz, but not at any other intermediate frequencies. (a) Is the pipe open or closed? (b) What is the fundamental frequency of this pipe? We first want to know what the ratio of one harmonic is to another. v = 2Lfn/n = 2Lfm/m Þfn/fm= m/n So for two harmonics fn/fm = m/n For a closed pipe the equation is the same. However, the harmonics are only odd. v = 4Lfn/n = 4Lfm/m Þfn/n = fm/m Þfn/fm= m/n
Only odd harmonics, so it is a closed pipe. f n = nf1 so f1 = f n/n = 264 Hz/3 = 88 Hz
What happens here is that the tuning fork oscillates at a single frequency, but that causes different harmonics of the tube to resonate. Remember there are only odd harmonics for a tube open at one end. ln= 4L/n ÞL = nln/4, so the difference between two different modes is given Ln+2- Ln = (n+2)l/4 - nl/4 = l/2 = .395 - .125 = .270 m Quality of Sound
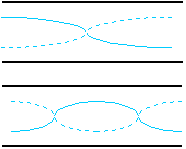
Interference and BeatsWe have talked about constructive and destructive interference of waves. Because sound is a wave, it demonstrates constructive and destructive interference. Consider two speakers as in figure 12-17. The two speakers send out waves of a single wavelength (frequency). These waves leave the speaker in phase. (That means that the trough of one wave leaves the speaker at the same time as the trough of the other wave, and the crests leave the speakers simultaneously, as well). If a listener is equal distance from each speaker then the waves will still be in phase and will exhibit constructive interference. This means that the sound will be louder because the amplitude will be the sum of the amplitudes of the two waves. Suppose though, that the listener is closer to one speaker than the other. If the listener is exactly 1/2 of a wavelength closer to one speaker than the other then the trough of one wave will arrive at the same time as the crest of the other wave, since one wave has traveled 1/2 of a wavelength farther. The two waves will then be out of phase, and destructive interference will occur. The amplitudes will cancel each other out and there will be no sound.
Both waves are at minimum (or) One wave is at its maximum and If one of the waves is shifted by exactly one wavelength, then the relative position of the two waves does not change. So constructive interference occurs when the listener is a distance of nl closer to one speaker than the other where l is the wavelength and n = 0,1,2,3... Destructive interference occurs when the listener is a distance of (n + 0.5)lcloser to one speaker than to the other speaker. Beats occur when two waves have slightly different frequencies. (See figure 12-18). When this happens, there are times when the waves interfere constructively and times when they interfere destructively. Since the constructive interference make the sound louder, and the destructive interference makes the sound softer, the sound will oscillate between soft and loud. This is called beats. The frequency with which beats will occur will be the difference in the two frequencies. fbeat = ïf1- f2ï
fbeat = ïf1 - f2ï 4 Hz = ï440 Hz - fïÞf = 444 Hz or f = 436 Hz. Doppler EffectWhen a source of sound and a listening device are not at rest with respect to each other, the pitch of the sound will change. This is known as the Doppler effect. It occurs because the wavelength (frequency)
of the sound changes because the source moves and "catches up" to the emitted wave. We denote the velocity of the sound source as vsand the velocity of the sound observer as vo. (Show wave fronts).
The derivations of all cases of the source and the observer moving are in the book and I will not repeat them here. Combining all of the equations gives
PROBLEM: An ambulance travels down a highway at a speed of 75.0 mi/h with its siren emitting a sound with a frequency of 400 Hz. What frequency is heard: (a) by someone standing still when the ambulance approaches? (b) by a passenger in a car traveling at 55 mi/h in the opposite direction as it approaches the ambulance? (c) by a passenger in a car traveling at 55 mi/h in the opposite direction as it moves away from the ambulance? 75 mi/h = 33.5 m/s, 55 mi/h = 24.6 m/s (a) f'= f(v)/(v-vs) = 400 Hz (343 m/s)(343 m/s - 33.5 m/s) = 443 Hz
(b) f'= f(v+vo)/(v-vs)=(400Hz)(343 m/s+24.6 m/s)/(343 m/s-33.5 m/s)= 475 Hz
(c) f' = f(v-vo)/(v+vs)=(400Hz)(343 m/s-24.6 m/s)/(343 m/s+33.5 m/s)= 339 Hz
PROBLEM: A man sitting in his car which is stopped sounds his horn that has a frequency of 500 Hz. The sound is reflected off of a car moving at 24 m/s toward the man. What frequency does the man hear? The wave hitting the moving car has a frequency of The reflected wave acts as if it is reemitted from the moving car, so Other TopicsSonic Boom
The Ear
Ultrasound
|
|
|
|
|
||||||||||||||||||||||||||
 Main Ideas:
Main Ideas:
 Sound waves are created from some source that is vibrating. The vibrating source creates longitudinal waves in some
medium that are detected by our ear of by an instrument.
Sound waves are created from some source that is vibrating. The vibrating source creates longitudinal waves in some
medium that are detected by our ear of by an instrument.
 PROBLEM: A camera focuses using ultrasound. If it focuses precisely at 20° C,
how far off (%) will it be at 0° C?
PROBLEM: A camera focuses using ultrasound. If it focuses precisely at 20° C,
how far off (%) will it be at 0° C?
 PROBLEM: A sound is measured to have a decibel level of 30 db. If the
intensity is decreased by a factor of 2, by how much does the intensity level change?
PROBLEM: A sound is measured to have a decibel level of 30 db. If the
intensity is decreased by a factor of 2, by how much does the intensity level change?

 The equations and concepts we used in chapter 11 for a string vibrating are used to understand stringed instruments. They are:
The equations and concepts we used in chapter 11 for a string vibrating are used to understand stringed instruments. They are:
 PROBLEM: The G string on a guitar has a fundamental frequency of 196 Hz
and a length of 0.62 m. If this string is pressed against the proper fret to produce the note C with a frequency of 262Hz, what is the distance between the fret and the end of the string?
PROBLEM: The G string on a guitar has a fundamental frequency of 196 Hz
and a length of 0.62 m. If this string is pressed against the proper fret to produce the note C with a frequency of 262Hz, what is the distance between the fret and the end of the string?

 PROBLEM: A tuning fork is set into vibration above a vertical open tube filled with
water. The water level is allowed to drop slowly. As it does so, the air in the tube above the water level is heard to resonate with the tuning fork when the distance
from the tube opening to the water level is 0.125 m and again at 0.395 m. What is the frequency of the tuning fork?
PROBLEM: A tuning fork is set into vibration above a vertical open tube filled with
water. The water level is allowed to drop slowly. As it does so, the air in the tube above the water level is heard to resonate with the tuning fork when the distance
from the tube opening to the water level is 0.125 m and again at 0.395 m. What is the frequency of the tuning fork?
 Every sound has a particular quality. The quality is the aspect of a
sound which distinguishes its overall characteristics. For instance, a piano and a trumpet may both be playing the exact same note with the exact same frequency and loudness, yet your ear can tell the difference.
What determines the quality of the sound? The quality of the sound depends on which overtones are present and what their amplitudes are. When a musical instrument plays a note the primary frequency that is
excited is the fundamental harmonic. However, other harmonics also resonate with different amplitudes. The number and magnitude of these other harmonics determines how "the sound is perceived by us." It is
the quality of the sound. Sounds we call noise tend to not just have higher harmonics of a fundamental harmonic resonating. They have a mixture of frequencies that do not necessarily have any relationship to
each other. There is no discernable pitch.
Every sound has a particular quality. The quality is the aspect of a
sound which distinguishes its overall characteristics. For instance, a piano and a trumpet may both be playing the exact same note with the exact same frequency and loudness, yet your ear can tell the difference.
What determines the quality of the sound? The quality of the sound depends on which overtones are present and what their amplitudes are. When a musical instrument plays a note the primary frequency that is
excited is the fundamental harmonic. However, other harmonics also resonate with different amplitudes. The number and magnitude of these other harmonics determines how "the sound is perceived by us." It is
the quality of the sound. Sounds we call noise tend to not just have higher harmonics of a fundamental harmonic resonating. They have a mixture of frequencies that do not necessarily have any relationship to
each other. There is no discernable pitch.

 PROBLEM: A particular piano note is supposed to vibrate at 440 Hz. A
tuning fork known to vibrate at 440 Hz is sounded at the same time as the piano key is struck, and a beat frequency of 4 beats per second is heard. Find the possible frequencies the string could be vibrating.
PROBLEM: A particular piano note is supposed to vibrate at 440 Hz. A
tuning fork known to vibrate at 440 Hz is sounded at the same time as the piano key is struck, and a beat frequency of 4 beats per second is heard. Find the possible frequencies the string could be vibrating.
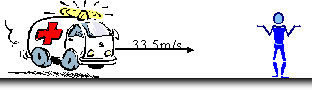
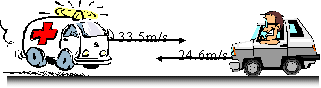

 When a source of sound moves faster than the speed of sound in a certain medium, the emitted wave fronts from the source have
overlapping wave crests. This creates a huge source of constructive interference known as a shock wave. The shock wave is heard as a loud "sonic boom". This will occur for any object moving faster than
the speed of sound for the entire period that the object is moving faster than sound. (Show wave fronts).
When a source of sound moves faster than the speed of sound in a certain medium, the emitted wave fronts from the source have
overlapping wave crests. This creates a huge source of constructive interference known as a shock wave. The shock wave is heard as a loud "sonic boom". This will occur for any object moving faster than
the speed of sound for the entire period that the object is moving faster than sound. (Show wave fronts).
 The ear is sensitive over a region from about 20 Hz to about 20,000 Hz.
However, it is not equally sensitive in all frequency regions. It is most sensitive to sounds about 2000 to 4000 Hz. It can hear such sounds at
intensity levels even down to about 0 dB, for a very good ear. However, sounds that are 100 Hz cannot be heard until they are at an intensity level
of 40 to 50 dB. Pain occurs when intensity levels reach about 120 dB. The "loudness" button on a stereo boosts the sounds at high and low frequencies when the sound level is turned down low, so that the ear can
hear them.
The ear is sensitive over a region from about 20 Hz to about 20,000 Hz.
However, it is not equally sensitive in all frequency regions. It is most sensitive to sounds about 2000 to 4000 Hz. It can hear such sounds at
intensity levels even down to about 0 dB, for a very good ear. However, sounds that are 100 Hz cannot be heard until they are at an intensity level
of 40 to 50 dB. Pain occurs when intensity levels reach about 120 dB. The "loudness" button on a stereo boosts the sounds at high and low frequencies when the sound level is turned down low, so that the ear can
hear them.
 Just as bats, and dolphins emit sounds which echo off of objects, so
humans have invented instruments which do the same. Since d = vt, we can measure the time it takes for a wave to be reflected off of an object to
measure how far it is from the emitted source. This is the basis for a number of technologies including ultrasound and sonar.
Just as bats, and dolphins emit sounds which echo off of objects, so
humans have invented instruments which do the same. Since d = vt, we can measure the time it takes for a wave to be reflected off of an object to
measure how far it is from the emitted source. This is the basis for a number of technologies including ultrasound and sonar.
