Chapter 16 Lecture Notes

Formulas:

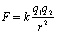
Constants:

e = 1.60×10^-19 C
k = 1/(4pe_o) = 8.988×10⁹ N×m²/C²
e_o = 8.85×10^-12 C²/(N×m²)

Demonstrations:

1. Electrostatics
• Rub rubber and glass rods with wool, etc.  Positive is defined as glass rubbed with silk.  Negative is defined as rubber rubbed with fur.
• Rub balloon on hair and stick to wall to show transfer of charge.
• Van de Graaff.
• Wintergreen Life Savers
2. Electric Field
• Bend a candle toward a negative plate.
• Field breakdown between two metal spheres. 

Electric Charges

     The Greek philosopher Thales observed that if a person rubbed amber (a petrified tree resin) with wool or fur, then the amber would attract small pieces of leaf or cloth.  Our word "electricity" comes from the Greek elektron - which means "amber."

Characteristics

Positive and Negative, Attractive and Repulsive

     There are two kinds of charge. Benjamin Franklin named them positive and negative and defined the charge on the rubbed glass rod to be positive. 

Demonstration: Positive and Negative Static Charges. Show how like charges repel and unlike charges attract. 

Like Charges Repel and Unlike Charges Attract.  This is one case where the phrase "Opposites Attract" is absolutely true. 

     When two thing are attracted this could occur for one of two reasons. Either they are of different charges, or one is charged and the other is attracted to it due to an induced polarizationof the charge. Induced polarization is when the charge within an object separates, so part of the object is slightly positively charged and some of the object is slightly negatively charged, even though the whole object has no net charge. 

Conserved

     We don't create or destroy charge, just transfer it.  In accelerators it can be created in pairs so that the total charge is always the same.  During any process, the net electric charge of an isolated system remains constant.  So if a charged object touches an uncharged object, some of the extra charge from the charged object transfers to the uncharged object.  But the total charge stays the same.  If the two objects are identical in composition, size, and shape, then after touching each other they will both have exactly the same amount of charge on them.

Quantized with Small magnitude, Including Atomic Origin

     Charges that we can observe are due to atomic electrons and protons.  Electrons are negatively charged and protons are positively charged. Electrons can move from one atom to another, so a negative charge means an excess of electrons and a positive charge is a deficiency of electrons. Ions are produced when an atom loses or gains electron(s).   The value of quantized charge is very small since e = 1.60×10^-19 C.  All charges come in integral multiples of e.  We measure charge using the unit (SI) of Coulombs (C). An electron has a charge of e = 1.60×10^-19 C, so there are (1.60×10^-19 C)^-1 = 6.25×10¹⁸ electrons per Coulomb.  Charge is usually measured in millicoulombs (mC) 1×10^-3 or in microcoulombs (mC) 1×10^-6.

Electrical Interactions

Conductors and Insulators

     Why don't you stand outside during an electrical storm hold a long tall metal object? Conductors easily conduct electric charge. Insulators do not easily conduct electric charge.  Metals are usually good conductors.  Plastics, rubber and wood are usually insulators.  Electrical cords illustrate this well.  The metal inside is a good conductor.  The rubber on the outside is a good insulator.

Charging by Contact and Induction

     What happens to multiple conductors and insulators next to each other?  What is the difference between objects touching each other and not touching?  When they touch, charge is transferred from one object to the other so that if the objects are the same shape and size, their charges equal each other.  When they are brought near, their charge moves within the object so the object becomes electrically polarized, but charge does not transfer from one object to another. 

We have an intuitive handle on "charge."

• We know we can give an object a "charge."
• We know we can transfer charge around (conduct, insulate).
• We know opposite charges attract [(+) to (-)].
• We know alike charges repel [(-) to (-) : (+) to (+)].
• We know of conductors and insulators.
• Atoms & Charge?
• Coulombs

     Here is a rather interesting observation. What is charge? – No one really knows. There are ideas as to what may cause charge but that involves "quarks," quantum mechanics, and a property called "color." – But that is a bigger can of worms. 

Show induced charge with rubber and glass rods. 

Force Between Point Charges

Coulomb's Law: Charles Coulomb (1736-1806)

     We want to know how strong the attraction or repulsion is between charged objects - this is given by Coulomb's Law that gives the strength of force between two charged objects. (Point charges – charge's physical size is much smaller than the distance between them.) 

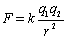
Know what it means.   If you double the charge on one object, the force doubles.  If you double the distance, the force decreases by a factor of four.  Coulomb's law gives the magnitude of the force directed along a line between the two charges.  The direction is determined from the sign of the charges.  To do problems with Coulomb's law, you must always use the absolute value of the charges, then determine the direction from the sign of the charges.  The constant k has the value of 8.988×10⁹ N×m²/C².  It is sometimes given in terms of the permittivity of free space e_o as k = 1/(4pe_o) where e_o = 8.85×10^-12 C²/(N×m²).

PROBLEM: (a) What is the force between the two point charges? (q1= +12×10-9 C, q2= -18×10-9 C) F= kq1q2/r2 = 2.2×10-5 N attractive  (b) Suppose q1 and q2 are connected by a conducting wire.  Now what is force?  When they are connected the charge flows from one to the other.  Because the two objects are the same size and shape, charge will flow until the total charge on each is the same. q1 + q2 = 6×10-9 C, so half is on q1 and half in on q2 = -3×10-9  C Then using Coulomb's Law, F = 8.99×10-7 N repulsive.

The Force is a Vector Force

     The electric force is a vector.  This means that when working with it, you must separate the components of the force into x and y components and add them up as vectors.

PROBLEM:  Suppose I have more than one charge. What is the total force on q3 from q2 and q1?  q1 = 6.00×10-9 C q2 = -2.00×10-9 C q3 = 5.00×10-9 C We know q = tan-1(3m/4m) = 36.9° F13 = 1.079×10-8 N ( away from q1 ) 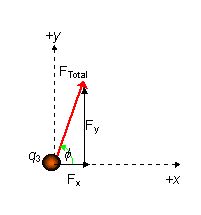F23 = 5.617×10-9 N ( toward q2 ) Now determine the total xy-components. SFy = F13y + F23y Fy = F13sin(36.9o) + 0 = 6.476×10-9 N SFx = -F23 + F12x Fx = -F23+ F13cos(36.9o) = 3.011×10-9 N F = Ö(Fx2 + Fy2) = 7.14×10-9 N tan(f) = Fy /Fx so force makes an angle of f = 65.1° with respect to the x axis.

     Note that you always find the force (direction and magnitude) from each individual charge first, then you add up the forces using vector components.

     The electric force is a force, like other forces we have learned about. Gravitational, centripetal, spring forces.  It can interact like all of the forces learned about in the first semester.  We'll do one example in class.

PROBLEM:     What is the angle and tension in the string?  At the end of the string the mass is m = 8.0×10-2kg and the charges are  q1 = 0.6×10-6C and q2 = -0.9×10-6 C. g=9.8 m/s2 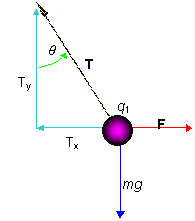Sum the forces acting on q1 SFy:  Ty – mg = 0  or  Tcos(q) = mg S Fx:  F  – Tx = 0  or   Tsin(q) = kq1q2/r2 (Divide to get tanq). tanq = kq1q2/mgr2= 0.275 q = tan-1(0.275) =  15.4o                           Plug into the first equation to get  T = .813 N

     The electric force is a much larger force than the gravitational force.  So why don't we feel strong electrical forces? - because most of matter is electrically neutral.  But what about the case when the matter is not neutral? 

PROBLEM:  Compare the electrostatic force to the gravitational force between the electron and the proton in a hydrogen atom.  Distance between the electron and proton is about r = 5.29×10-11 m. The masses are me=9.11×10-31kg. mP=1.67×10-27kg. qe = qP = 1.6×10-19 C Electrostatic Force is given by Coulombs law and is: F=kqeqp/r2 F = (8.99×109 N×m2/C2)(1.6×10-19 C)2/(5.29×10-11 m)2 = 8.22×10-8 N. Gravitational Force is given by Newton's law of Universal gravitation and is:  F=Gmemp/r2 F = (6.67×10-11 N×m2/kg2)(9.11×10-31kg)(1.67×10-27kg)/(5.29×10-11m)2  F  =  3.63×10-47 N. Ratio = 2.26×1039.  In a hydrogen atom, gravity plays basically no role.

Electric Field: Michael Faraday (1791-1867)

Electric Fields and Test Charges

     An electric field is a vector quantity meaning it has a magnitude and a direction.  The direction is defined as the direction of the electrical force that would be exerted on a small positive test charge.   The magnitude of the electric field does not depend on the test charge.  A test charge doesn't disturb field.  A field leads to a force on a charged object.

Electric Fields from Various Objects

• From a point charge. F = kq_oq/r² and since E=F/q_o, E = kq/r²
• A parallel plate capacitor makes a uniform electric field
• We will look at other electric fields in the next chapter.

Electric Field Lines (Acting at a distance)

We illustrate electric fields with electric field lines.  (Draw objects with field lines)

1. They point in the direction that a positive charge would move.
2. Their density is proportional to the magnitude of the electric field.

     Show how charged particles move in an electric field. A constant electric field, usually produced by a parallel plate capacitor, creates the same kind of motion as a constant gravitational field.. 

Bend a candle toward a negatively charged plate.

PROBLEM.  A particle with positive charge moves in a certain direction.  What will particle with same mass and negative charge do?  How about one with twice the charge?  What about neutral?  Why?  F = ma = qE.

Force From an Electric Field (Vector Addition)

   Electric fields can exist due to a variety of sources.  There may be a small charge nearby, or from a capacitor nearby.  If a charge is placed in an electric field, it then feels a force.  How big is the force?  It depends on the size of the field and on the size of the charge since F = Eq.  Remember that both the force and the field are vectors.

PROBLEM:   (a) What is the total electric field 30 cm above point charge q2 if q1 = -25×10-6 C and q2 = 25×10-6 C?   The angle that E1 makes with the x-axis is given by: cosq = (40cm)/(50cm) or q =36.9°. Electric Field from q1: E1= kq1/r2 = (9.0×109 N×m2/C2)(25×106C)/(0.50m)2  = 9.0×105 N/C Electric Field from q2: E2= kq2/r2 = (9.0×109 N×m2/C2)(25×106C)/(0.30m)2 = 2.5×106 N/C Sum the Vector xy-components: SEx = E1x = E1cos(36.9o) =7.2×105 N/C S Ey = E2-E1y = E2 - E1sin(36.9o) = 2.0×106 N/C ETotal= Ö(Ex2 +Ey2) = 2.1×106 N/C The angle the field makes with the x axis is given by: f= tan-1Ey /Ex = 70° (b) What is force on a particle there?  It depends on the charge of the particle you put there since F = qE.

Electric Field From a Point Charge

PROBLEM:  Where is electric field zero between two point charges? You must use magnitudes (absolute values of the two charges) to solve this problem.(q1=-2.5×10-6 C, q2 = 6×10-6 C). Where does E1 = E2? Maybe at some position "x?" We will call the location of q1 equal to 0m, and q2 equal to 1.0m. E1 = E2 kq1/(r1)2 = kq2/(r2)2                 r1 = x;    r2 = 1 – x kq1/x2 = kq2/(1 - x)2 x2(q2-q1) + x(2q1) - q1 = 0 Solutions for Equations:  ax2+bx+c=0 Quadratic Equation: 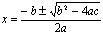    Use quadratic formula and plug in absolute values of the charges: q2 - q1 = 3.5×10-6, and - q1 = -2.5×10-6 x = (-5 ±Ö{52-4(3.5)(-2.5)})/7 = (-5 ± 7.7)/7 = .39m or -1.8m It is -1.8m because that is the only place that a positive test charge will not move.  The answer can be checked by plugging into Coulomb's Law. There is an easier way to solve this problem.  The electric field is zero where a positively charged particle would feel no force since F = qE .  If you think about if for a moment you will realize that this would have to be to the left of q1.  So setting the distance x to the left of q1 we get, q1/x2 = q2/(1+x)2 Take square root and solve x = Ö(q1)/{Ö(q2) - Ö(q1)}

PROBLEM/DEMONSTRATION: When will we get a spark between the two metal spheres on the charge demonstration?  Dielectric strength of air is 3.0×106 N/C =V/m.  A spark happens when electric field strength equals the dielectric strength of air.  E field is kq/r2 + kq/r2 where r is ½ the distance between the balls. q=Er2/2k  = 1.7×10-4 (r2) Coulombs.  So if r is .02m (=2 cm) then q= .06mC.

Field Inside and Field Lines Outside of a Conductor

     There is no field inside of a conductor.  All of the field lines are perpendicular to the conductor at the conductor's surface.  Like charges repel and they can move easily so they move away from each other.  Suppose there are two conducting spheres each with 6mC of positive charge.  Where is charge located on the two spheres? 

• +6 on outside of inner sphere.
• -6 on inside of outer sphere.
• +12 on outside of outer sphere