Chapter 17  Lecture  Notes

Formulas: 

qV = UE               Definition of electric potential W = Fd(cosq)      Definition of Work W = -DUE           Relationship between work and potential                        energy for work  done by a conservative field. V = Ed                 Potential for a constant electric field.  V = kQ/r              Potential of a point charge Q = CV                 Charge on a capacitor C = keoA/d          Parallel plate capacitor k = Eo/E              Dielectric Constant E = (1/2)CV2        Energy stored in capacitor

Constants:

1 N-m = 1 Joule             1 N = 1 kg-m/s²              k = 8.99´10⁹ N-m²/C²

Electric Potential Energy & Potential Differences

     Recall that near the surface of the earth, the acceleration of gravity is a constant. This is analogous to saying that the gravitational field is a constant. Therefore, a constant electric field interacts with charge the same way a constant gravitational field interacts with mass.  Positive charge plays the role of mass.  (Blame Benjamin Franklin).  There is potential energy in gravity, and in electricity.  A constant electric field can be produced with a parallel plate capacitor.

In General

     The electric potential is not the same as the electric potential energy.  It is related to the electric potential energy by the formula

V= U_E/q       or      qV = U_E      

where V is the electric potential and U_E is the electric potential energy. Note that this is a scalar so potentials can be added like scalars. The SI Units of Electric Potential is joule/coulomb = volt (V).  (Alessandro Volta –1745-1827) 

     The electric field, like the gravitational field, is a conservative field.  That means the work done to move a charged object from one point to another in an electric field does not depend on the path taken, but just on the total displacement.  We don't have any absolute reference frame for electric potential, just like we didn't have one for gravitational potential, and like gravity we can only measure changes in potential energy.

qDV=DU_E             (Remember that the symbol DU means U_final - U_initial.)

Also recall that potential energy can only be defined in a conservative field.  There is no such thing as potential energy in a nonconservative field.  The  work done to move a charge in a conservative field, like a gravitational or electrical field is given by: 

W = Fd(cosq)       In a constant conservative field (like gravity)

W = Eqd(cosq)     In a constant electric field (which is always conservative).

     Recall from Physics-121 that we can relate the change in potential energy to work done.  For instance, if I hold onto a ball and lower it in a constant gravitational field the work done by my hand is given by W_Hand = DU_G.   But the work done by gravity on the ball when I lower it is W_G = -DU_G.  The work done by the conservative field on an object is always the negative of the change in potential energy. 

     The book is not precise when talking about work done by a field and work done against a field.  On page 506 the author says that the work done by the electric field to move an object from b to a is given by W =qV_ba.  Note, however, that

W = qV_ba = q(V_b - V_a) = q(V_b - V_a) = q(V_initial- V_final) = -q(V_final-V_inital) = -qDV.

So by writing V_ba instead of DV the author has subtly avoided using this minus sign.  I write equation 17-2 using DV instead of V_ba so I get

DV =  DU_C/q = -W_C/q = -Eqd(cosq)/q = -Ed         (Note the minus sign).

The bottom line is that the formulas W=Fd(cos q), V=U_E/q, and     DV=DU_E/q are always true.  But the relationship between the change in potential energy (DU_E) and the work done (W) depends on whether I talk about the work done by the field or by an object against the field.  If it is the work done by the conservative field I get W_C =  -DU_C.  But if it is work done by an object against the field, I get W = +DU_C.  Everything learned about work and potential energy in Physics-121 can be applied in the case of the electric field.

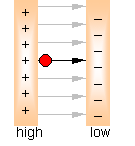PROBLEM: Work and Electric Potential: A proton with a charge of 1.6´10-19C is released from rest in a uniform electric field of magnitude 8´104 V/m. After the proton has moved 0.5 meters: (a) What is the change in electric potential. DV = -Ed = -4.0´104 V (b) What is the change in potential energy? Many problems in the book dealing with the work done by the electric field start with this step. DUE  = Uf - Ui = qDV = -6.4´10-15 J. The sign says that we are at a lower potential.  (Again remember gravity). (c) What is the speed of the proton? We use conservation of mechanical energy. KEi + Ui  = KEf + Uf  Þ  KEf = Ui - Uf = -DUE DUE = K = 1/2(mv2).   Solve for v and get v2=7.66´106 m2/s2 v = 2.8´106 m/s

Potential of a Point Charge

     The point charge creates an electric potential. We need to use calculus to determine the potential because the force varies as r changes (not a constant field). We find

V = kq/r.

Note that this means that the potential from a point charge at an infinite distance away is usually chosen to be zero, since 1/¥ = 0.

PROBLEM:  How much work does it take to move a charge of  q = -3.0mC to a point .50 meters from a charge of Q2= 20.0mC? r1=¥ , so W = DUE = qDV = q(kQ2/rfinal – kQ2/rinitial), W= (-3.0mC)(8.99´109 N-m2/C2)(20.0mC)/0.5m = -1.08 J. What if I add another charge as the figure shows? From above, the work to move q=-3.0 mC to a point .50 meters from a charge of Q2=20.0 mC is -1.08 J.  Now we must move Q1to within .3 m of Q2 and to within .6 m of q.  The work to move it to within .3 m of Q2is the same calculation as above with r2 = .3 m and r1=¥, W2 = DUE = Q1DV = Q1(kQ2/r2 – kQ2/r1) = 3.00 J and finally, the work it takes to move Q1 to within .6 m of q is given by the same equation,  W3 = DUE = Q1DV = Q1(kq/r2 - kq/r1) = -0.22 J So the total work is given by W =W1 + W2 + W3  = 1.70 J

The Electron Volt

     A unit of energy (NOT SI) is the electron volt. The amount of energy one electron gains when it moves through a potential of 1 volt.

1 eV = (1.6´10^-19 C)(1 V) = 1.6´10^-19 Joules.

Won't use this much now, but will be used later.  Used in all areas of atomic, nuclear, and particle physics because joule is too large. 

Equipotential Surfaces

     An equipotential surface describes an imaginary surface where the electric potential is the same everywhere - like a topographical map.  Equipotential surfaces are always perpendicular to electric field lines.  The surface of a conductor is an equipotential surface.  No work is required to move a charge at a constant speed along an equipotential surface.  (Like horizontally in a gravitational field.)

Integration of Concepts

We have defined four concepts associated with electric charge.  They are:

(1) The force on a point charge F
(2) The electric field E
(3) The potential energy of a charge acted on by an electric force U_E
(4) The electric potential V

For any number of point charges, we can calculate F, E, V, and U_E. There are relationships.  F = q E, U_E =qV.  To go from F to U_E and from E to V require calculus.  These four basic equations make up Maxwell's laws named after James Clerk Maxwell, an English physicist who discovered them in about the middle of the last century.  We will encounter special cases of the remainder of Maxwell's equations later in the course.

Capacitors

Definition of Capacitance

     A capacitor consists of two conductors of any shape which are close to each other but not touching.  A capacitor can store charge on the plates.  Capacitors usually store the same amount of charge on each plate, with one plate being positively charged, and one being negatively charged. Because of this charge the electric potential of the positive plates is higher than that of the negative plates. Physicists want to be quantitative, so we ask how much higher.  We get the relationship q=CV.  Given a certain physical set up, C is a constant.  It can only change C by changing the set up.   The SI unit for C are C/V = farad (F). 

For a parallel plate capacitor we find C = e_oA/d where A is the area of the plates and d is the distance between them.

PROBLEM:   If a capacitor has 3.5 mC of charge on it and an electric field of 2.0 kV/mm is desired if they are separated by 5.0 mm of air, what must each plate's area be? (2.0 kV/mm)(1000V/kV)(1000mm/m) = 2´106 V/m Q = CV = CEd = (e0A/d )Ed = eoAE A = Q/Eeo = (3.5´10-6 C) / {(8.85´10-12 C2/N×m2)(2´106 V/m)} = 0.20 m2

     To solve many more difficult problems with capacitors you must remember that charge is always conserved, and think about what happens to the charges.  If all the connections between the two plates of the capacitor are disconnected, we say the capacitor is isolated and the charge remains constant. If a battery stays connected to the capacitor, then the voltage will stay constant.

PROBLEM: A 2.50mF capacitor is charged to 1000 V and a 6.80mF capacitor is charged to 650 V.  Then the positive plates are connected to each other and the negative plates are connected to each other.  What will be the potential difference across each and the charge on each?   Charge on first capacitor is Q1 =C1V1 = (2.50´10-6 F)(1000 V) = 2.50´10-3 C Charge on second capacitor is Q2 =C2V2 =(6.80´10-6 F)(650 V) = 4.42´10-3 C Total charge is Q = Q1 + Q2 = 6.92´10-3 C                                            Now let Q1¢ be the new charge on the first capacitor. Then the new charge on the second capacitor is (6.92´10-3 C - Q1¢).  Because the plates are connected, the potential difference across the capacitors will be the same, so Q1¢ = C1V = (2.50´10-6 F)V Q2¢ = 6.92´10-3 C - Q1¢ =C2V = (6.80´10-6 F)V Plug the first equation into the second to get 6.92´10-3 C - (2.50´10-6 F)V = (6.80´10-6 F)V 6.92´10-3 C = (2.50´10-6 F + 6.80´10-6 F) V V = 744 V Plug this into the two equations to get Q1¢ = 1.86 ´ 10-3 C and Q2¢ = 5.06 ´ 10-3 C

Show charge on balls and spark again with and without dielectrics.

A Dielectric In a Capacitor

     If we can increase C, then we can store more charge for a given potential.  One way of doing this is putting in a dielectric material which reduces the electric field in the material when the capacitor is isolated.  The ratio of electric field before adding the dielectric to electric field after is called the dielectric constant k.  k=E_o/E.  Dielectric constants are listed in table 17-2.

V=Ed

V/d = E = E_o/k

Since E_o = q/e_oA, then q =(ke_oA/d)V or C=ke_oA/d compared to C = e_oA/d  without the dielectric.  So adding a dielectric with k > 0 increases the capacitance by decreasing the electric field inside the capacitor for the same amount of charge on the plates (that is for an isolated capacitor).

PROBLEM:  A parallel plate capacitor is fully charged at a potential V.  A dielectric with constant k =4 is inserted between the plates while the potential remains constant.  What happens to the amount of charge stored?  (It increases by a factor of 4).

PROBLEM:   Suppose a parallel plate capacitor has plates that are 2.0 cm by 3.0 cm which are separated by 1.0 mm.  The maximum electric field in air, called the dielectric strength of air, is 3.00´106V/m. (a) What is the maximum charge that can be placed on this capacitor? C = eoA/d = (8.85´10-12 C2/N×m2)(.02 m)(.03 m)/(.001m) = 5.31´10-12 F C = 5.31 pF VMAX = EMAX d = (3.00´106V/m)(0.001m) = 3.0´103 V  Q = CV  = (5.31´10-12F)(3.00´103V) = 1.59´10-8C = 15.9 nC (b) Suppose paper with a dielectric constant of k = 3.7 and a dielectric strength of 16 ´ 106 V/m is placed between the plates.  How much charge can it hold now? C = keoA/d = 3.7(5.31´10-12F) = 1.96´10-11F VMAX = EMAX d  = (16.00´106V/m)(.001) = 1.60´104V Q = CV = (1.96´10-11F)(1.60´104V) = 3.14´10-7C = 314 nC (It holds 20 times more charge with the space filled with paper).

Energy Stored in a Capacitor

   The energy stored in the capacitor is the amount of work it took to put the charge on the capacitor.  This is the work done against the capacitor to charge it up, not the work done by the capacitor. Suppose we move charge from one plate to the other.  The work required to do that is given by the change in potential energy, or 

W  = DU_E=D(qV), so DW = DqV.   

     Initially V is 0 so it takes almost no work to move a charge across the plates.  (It is an equipotential surface).  However, as soon as we move some charge we now have a potential and V = q/C. By the time we are moving the last bit of charge we are doing work against the full voltage.   The work required, then, is the average of the work required to move the first charges and the work required to move the last charges.

W = E = (1/2)(0 + qV) 

and since q = CV, 

E = (1/2)CV² 

E = (1/2)(ke_oA/d)(Ed)²

PROBLEM:  An electronic flash works by storing energy in a capacitor and releasing the energy very quickly.  Suppose an electronic flash has a 750 mF capacitor and a potential of 330V.  What is the energy stored? E=(1/2)CV2 = 1/2(750´10-6)(330)2 = (C/volt)(volt)2 = 41 Joules. Assuming the flash lasts for 5´10-3 seconds, what is the power used? P =E/t   = (41 J)/(5´10-3) = 8200 watts.