Chapter  21 Lecture Notes

Formulas: 

  F = BAcosf
  Faraday's Law:  E = -N DF/Dt
  E = Bvl
  E = NABwsinwt
  M = (N₂F₂)/I₁                         E ₂ = -MDI₁/Dt
  L = NF/I                                   E = -LDI/Dt
  Solenoid:   L = m_on²A l         Energy = (1/2m_o)B²Al    
  Energy = (1/2)LI²
  Energy Density = Energy/volume = (1/2m_o)B²
  I_p/I_s =V_s/V_p = N_s/N_p
  X_c = 1/2pfC 

Constants:

1 T = Newton-second/(coulomb-meter) = N/A×m
1 W = 1 T-m²                           m_o = 4p´10^-7 T×m/A 

Demonstrations:

• Induce current by changing magnetic field through wire loop
• Induce current through precision galvanometer and use slide projector
• Generator and counter-torque
• Magnet and pendulum and eddy currents
• Magnet on copper and eddy currents.
• Show induced eddy currents by dropping a magnet through a tube 

Introduction

     The main emphasis of this chapter can be summed up in one sentence.  A Changing Magnetic Flux induces an emf (electromotive force, or voltage difference).  This statement immediately brings up three questions that we need to answer?

1. What is a magnetic flux? 
2. How do you change it? 
3. What are the consequences of the induced emf and what is it's polarity? 

Magnetic Flux

Definition: What is Magnetic Flux

     Suppose we have a magnetic field going through a surface. Then the perpendicular component of the magnetic field going through the surface times the area of the surface is called the magnetic flux. 

F = BAcosf          SI Units:  T-m² which is a Weber (Wb) - Wilhelm Weber
                     f is the angle between the normal to the surface and the magnetic field

     Suppose the object in question is a loop of wire. Then the area (A) has a magnitude equal to the area inside of the wire loop which contains the magnetic flux and a direction perpendicular to face of the wire loop.

PROBLEM:  A loop of wire with a radius of .50 m is placed in a magnetic field of .60 Tesla. What is the flux through the wire loop when the face of the loop is (a) perpendicular to the magnetic field, (b) parallel to the magnetic field, and (c) at an angle of 30° to the magnetic field as shown in the figure?  (The figure is the view looking down on the wire loop)   Area of the loop is pr2 = 0.79 m2 f = 0° f = 90° f = 60° F = BA cosf cos(90°) = 0 F = BA cos(60°) F = (0.60T)(0.79m2)(1) so F = 0 F = (0.60T)(0.79m2)(0.5) F = .47 Wb   F = .24 Wb

How can we change F?

1. We could change the Area.  When we do that we get something called "Motional emf" that is discussed in the book. 
2. We could change f.  We usually do that by rotating a wire loop(s) in a magnetic field.  When we do that we get a generator - which is discussed in the book. 
3. We could change B.  When we do that we get the phenomena of inductance (leading to transformers) talked about in the book. 

So all of the topics in the first half of chapter 21 are simply results of the fact that a changing magnetic flux induces an emf and an emf can produce a current.

What are the consequences of the induced emf?

     When we change the magnetic flux we always get an induced emf.  In addition, if there is a closed path for charged particles to flow, we also get a current since emf's lead to current.  Eureka!  We've got electric current simply from a changing magnetic flux.  The electric current flows in such a direction as to oppose the change in magnetic flux. 

Faraday's Law and Lenz's Law

     Now we want to make this more quantitative.  What is the magnitude of the emf created when the flux changes?  Suppose we have a coil of wire.  The emf induced by a changing the magnetic flux is given by Faraday's Law.

E = -NDF/Dt

     It is easiest to use the magnitude of the emf from Faraday's law and determine the direction of the induced emf from Lenz's Law. 

     What is the direction of the induced current?  According to Lenz's law, the induced current produces a magnetic field that opposes the change in flux causing the emf.  That is the purpose of the minus sign in Faraday's law.  It indicates that the induced emf is such that the magnetic force F acts to oppose the change in magnetic flux.  We'll see how that works.   What matters is the flux inside the wire loop.  That is the defined area. 

There are three steps to solving problems with Lenz's Law. 

1. Determine the direction of B.
2. Determine if F is increasing or decreasing.
3. Choose the current direction to oppose the change in F. If flux is decreasing choose current to increase B.  If flux is increasing, choose current to decrease B.

PROBLEM:  A coil of 200 turns is wrapped on an 18.0 cm by 18.0 cm frame.  The total resistance of the coil is 2.00W.  A magnetic field that is perpendicular to the plane of the coil is change from 0.500 T to 0 Tesla in 0.800 s.  Find the magnitude of the induced emf. E = -NDF/Dt = -ND(BAcosf)/Dt = -NADBcosf/Dt E  = -200(18 cm)2(1 m/100 cm)2(0 - 0.500 T)(cos(0°))/0.800 s E = 4.05 V What is the current in the wire? E = IR I = E/R = 4.05 V/2.00W = 2.03 A Here I am changing the magnetic field, but I could change the area or the angle and change the flux.

Applications and Examples

Motional EMF

     This is the simplest case of Faraday's Law.   A conductor moving in a magnetic field creates an EMF (a potential difference). Explain direction using Lenz's Law. 

E = DF/Dt = BDA/Dt = BLd/Dt = Blv

Another way to look at it is that the magnetic field moves the charges         

I want you to see two important things about this situation.     

     First, we know that if we have a current in a magnetic field then a force is created.  So the force the charged particles in the rod feel is F=qvB, or in terms of current, F=ILB. The direction of the force is from left to right in this picture.  So to create a velocity from right to left, we need an external force, like gravity or a spring or my hand pulling it. 

     Second, we see from the above force equations that F/q = vB.      

Recall from our chapter on electricity, we defined the electric field as E = F/q, so we can write this equation can be written as 

E = Bv 

This illustrates an extremely important principle. A changing magnetic flux produces an electric field. 

     (Special Note:  Motional emf can actually be explained without introducing magnetic flux and Faraday's Law, so some books use this idea to develop Faraday's law.  The idea of a motional emf, then, can be thought of using Faraday's law, or simply using ideas the ideas about the changing magnetic flux.) 

PROBLEM:  Suppose you are driving along within the earth's magnetic field with a vertical component downward of 5.0´10-5 T at 75 MPH.  The car is about 2 meters wide. What is the induced emf and is it positive on driver's or passenger's side? A)   Driver's side by RHR. B) Calculate the induced emf: E = Blv = (5.0´10-5 T)(2 m)(75 MPH)(1/3600 hour/s)(1609 m/mile) E = 3.0´10-3 V. Recall that a little dry cell battery is 1.5 volts, so this is not very much.

This is similar to any problem with motional emf.  If you knew the emf in the above figure, how would you figure out the current in the circuit? What if you were told that there was no resistor but just a copper wire for a loop?  What would you do then?

Work and Motional EMF

     If we have an emf then we have E = IR and we have power dissipated in the resistor. (We may be lighting a light bulb). Where is this power coming from? Energy is supposed to be conserved. Well, the rod doesn't move on its own. It takes energy (or work) to move it. In fact, the RHR shows that the current in the rod creates a force that wants to stop the rod.  F = ILB sinq.  It takes an external agent to supply the energy/work to light the bulb.

The Electric Generator

   Motional emf is one way to create electricity.  But the wire would have to be long, so there is a better way.  It still uses Faraday's Law. Instead of changing the area, we will change the angle f.  How do we do this?  We make a generator.  A generator changes mechanical energy (of falling water, steam, etc.) into electrical energy.  It is exactly the opposite of a motor that changes electrical energy into mechanical energy.  Consider the following figure, and look at the two vertical arms of the wire.

     The current direction is given by the right hand rule using v and B.  The charges in the wire feel this force (in the direction of I) which gives rise to the current.  The magnitude of the emf is given by the equation for motional emf that we derived. 

E = BLv_^ =BLvsinq                   q is the angle between the velocity and B.

For both wires, and many turns

E = 2NBLvsinq              

If the coil is rotating with constant angular velocity, then q= wt.

Also angular equations, v = wr = ww/2

E = 2NBLw(w/2)sinwt

E = NABwsinwt

Recall that the peak current is given by the numbers in front of the sin function, or

E_o=NABw

The current is going back and forth in the wire.  If we use slip rings to make the connection we have an ac generator. With split ring commutators, we have a dc generator. 

Countertorque and Eddy Currents

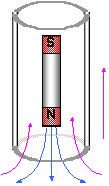     So far we have developed one concept in this chapter and discussed two consequences of that concept.  A changing magnetic flux creates an emf.  The consequences of that are that an emf can produce a current which creates a magnetic field opposing the change in flux.  There is more to the story than this, however.   The consequences of this can be quite dramatic.  For instance, we know that the magnetic field from the induced current opposes the changing flux.  This often produces a force opposing the motion involved. You actually don't even need a loop of wire to feel this opposing force.  Any conductor can have localized areas of current loops called Eddy currents.  These will create magnetic fields and opposing forces.  Let's see the consequence of this opposing force. 

Demonstration:  Drop magnet and non-magnet through tube.

This current comes from Lenz's law and acts like a little dipole magnet slowing the progress of the dropped magnet.

Demonstration:  Slowing Pendulum and magnet over copper.

All of these things demonstrate that the currents produced from changing magnetic fluxes can actually oppose the force creating the changing flux.

     Another example of this is counter-torque in a generator.  As I crank a generator, I am rotating a coil and creating a current.  We know that a rotating coil with a current passing through it feels a torque. The torque is in the opposite direction of the rotation of the coil. The torque it feels is called counter-torque.

Demonstration:  Electric Generator with and without light bulb.

     When I unscrew the light bulb, there is no more counter-torque opposing my motion and it becomes easier to rotate the crank. Another way of thinking of this is that when there is current flowing, I am now doing work to turn the crank against friction, and doing work to create electrical energy.  Just like it takes work to keep the bar moving in motional emf, it takes work to keep the coil rotating for a generator.  This is conservation of energy - mechanical energy (or heat energy) into electrical energy. 

Where does the energy come from to drive the motor?  From falling water or steam, etc

Counter-emf of a Motor

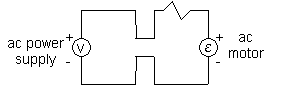     We talk briefly about motors again.  A motor changes electrical energy into mechanical energy.  The changing magnetic flux of a motor as it turns, produces an emf that is trying to stop the motor.  We call this back-emf or counter-emf. So there are two source of emf on a motor.  The emf driving the motor (V) and the back emf (E).  The greater the speed of the motor,the greater the back emf. 

I= (V-E)/R.  

So as the motor speeds up and E increases, current actually decreases.

PROBLEM:  Suppose that a motor running at 1200 rpm has a counter emf of 50 V.  What is the counter emf when the motor is running at 2000 rpm? We know Eo = NABw.  Since the magnetic field, the area and the number of wires doesn't change, then the back emf is only proportional to w. E1200/E2000 = w1200/w2000 50 V/ E2000 = 2p(1200 rpm)/{2p(2000 rpm)} E2000 = (50 V)(2000)/(1200) = 83 V

 

Inductance

We have talked about motional emf and generators as examples of changing magnetic fluxes, changing A and f, respectively.  Now we talk about changing B.  What happens when we do that.   Look at the figure below. 

     When we change a current in one coil, this changes the magnetic field in that coil.  The changing magnetic field in the first coil produces a changing magnetic field in the second coil.  That produces an emf in the second coil which causes a current in the second coil. This is called mutual inductance since the changing current in the first coil induces a current in the second coil.  The flux in the second coil is proportional to the current in the first coil.  The proportionality constant is called the mutual inductance.

N₂DF₂ = MDI₁      SI Units of M are T-m²/A = W/A = V-s/A = Henry (H)

M = (N₂DF₂)/DI₁   (since V = W/s)

From Faraday's Law we know

E ₂ = -N₂DF₂/Dt   (substitute above in)

E ₂ = -MDI₁/Dt

Also, as current increases in a coil itself, the flux changes and an emf is produced. This is called self-inductance.  (Same derivation with L used).

E = -LDI/Dt                       where L =NDF/DI

What is the self-inductance of a solenoid?

L = NDF/DI = ND(BA)/DI

L = ND(m_onIA)/I                                   n = number turns/length =N/l

L = ND(m_oNIA)/DI l

L = Nm_oNADI/DI l = m_oN²A /l

     Where does it all end?  A single solenoid has only self-inductance.  Two of them have self-inductance and mutual-inductance. Always remember that something has to drive the system.  Usually one of the inductors is connected to an ac or dc source and is driving the system.  But both are always opposing any change in flux.

     Finally, there is energy stored in an inductor.  It takes work to establish current in the conductor since Lenz's Law says that the inductor doesn't want to add current.  Again, like with capacitors, deriving the equation requires calculus.

Energy = (1/2)LI².  (always true)

For a solenoid:

Energy = (1/2)m_on²AlI ²     with B = m_onI,  

Energy = (1/2m_o)B²A l

We can generalize this to the energy stored in any magnetic field.  We usually write this as the energy density (u) which is the energy per volume.

u = (1/2m_o)B²

Transformers

An emf in 2 is induced from 1 using

E ₂ = -N₂DF/Dt

In coil 1, we have self-induction:

E ₁ = -N₁DF/Dt. 

Transformers are designed so that the same flux goes through both coils so DF/Dt is the same.

E ₂/E ₁ = N₂/N₁           V_s/V_p = N_s/N_p 

If the secondary has more turns it is a step up transformer, and if it has less turns it is a step down transformer.  Transformers change voltage easily. This is one of the principle reasons it is preferred over dc.  They only work for ac current.

Energy must be conserved so P₁ = P₂

I₁V₁ = I₂V₂   or       I_p/I_s =V_s/V_p = N_s/N_p  

So if the voltage is stepped up, the current is stepped down.  Note the inverse relationship here.

PROBLEM:  The input to the primary coil of a transformer is 120 V while the current in the secondary coil is 0.10 A.  When 60.0 W of power are delivered to the circuit attached to the secondary coil, what is the voltage across this coil? P = IV ÞV =P/I = (60.0 W)/(0.10 A) = 600 V If the primary coil has 20 turns, how many does the secondary coil have? Ns= NpVs/Vp = (20)(600 V)/(120 V) = 100

     Transformers are used to transfer power from the power company to homes.  The resistance between the points is constant.  Since power lost in a resistor is I²R, we try to minimize I when transferring electricity over a long way. So the power company steps up voltage (lowering the current) at the place where electricity is produced and steps it down (raising the current) when they want to use it.  There is a transformer sitting outside of your house.

PROBLEM:  Suppose 10 MW of power is being transported over a power line that has a resistance of 0.200 W.  How much power is lost along the line if the voltage of the line is (a) 120 V, (b) 24,000 V?      (Note that there are two different ideas about power involved here.  The first idea is the total power being transported which can be written as P = IV. The second idea is the power lost in a transmission line.  The power lost in the transmission line is not P=IV where V is the voltage of the line, because the voltage of the line is not the same thing as the voltage drop from one end of the line to the other.  Remember that power is voltage drop across a device times the current through the device, but the voltage drop across the line is not the same thing as the voltage of the line!) (a) P = IV I = P/V = (10´105 W)/(120 V)  I = 8.3´104 A P = I2R = (8.3´104 A)2(.200 W) P = 1.4´109W  (more than being sent) (b) I = P/V = (10´105 W)/(24,000 V)  = 4.17 A P = I2R = (4.17 A)2(.200W) P = 3.5 W

Capacitors in ac Circuits

There are two important concepts about capacitors in circuits. 

1. In a dc circuit, capacitors do not allow current through, but in an ac circuit they do.
2. The capacitor affects the circuit in two ways
• The phase of the current changes through a capacitor.
• The resistance of the capacitor (capacitive reactance) changes with different frequencies.

Think about what is happening with the charges.

PROBLEM:  An 8.00 mF capacitor is connected to the terminals of an ac generator with an rms voltage of 150 and a frequency of 60.0 Hz.  (a) Find the capacitive reactance and the rms current in the circuit.  (b) What happens if the frequency is doubled? (a) Xc = 1/2pfC = 1/(2)(3.1416)(60.0)(8´10-6 F) = 332 W VR = IR = IXc I = V/Xc  = 150 V/332 W = 0.452 A (b) Then the capacitive reactance is halved, and the current doubles. Similarly in an AC circuit, the impedence of an inductor changes with frequency.  We find XL = 2pfL.