|
Chapter 23 Lecture Notes
 Formulas: Formulas:
 Demonstrations: Demonstrations:
- Blackboard Optics
- Mirror Mirage
- Mirrors and lenses to show
The Reflection of Light and Mirrors
Wave Fronts and Rays
A wave front is like the ripples in a pond when a rock is thrown in. The distance between the ripples is the wavelength (l). The wave fronts are curved. Rays are lines drawn in the direction the wave front is moving. Rays are perpendicular to the wave front. A long distance from the source,
the wave fronts are flat (i.e. plane waves). The rays are all parallel to each other. We use this idea in optics. (e.g. Rays from the sun are all parallel to each other.)
Reflection of Light
The Law of Reflection says:
- The incident ray, the normal, and the reflected ray are all in the same plane.
- The angles are equal qr = qi. Always measure the angles from the normal to the surface. Do
not measure the angle from the surface face itself.
Light reflects off a smooth surface. If you see a reflection, the surface demonstrates "specular reflection." Many surfaces are microscopically rough, like the pages of a book.
We don't see any reflection off of the pages.
What would the reflection off of a sphere look like? The angle of reflection is determined
by drawing a plane tangent to the surface of the sphere with the reflected and incident angles the same.
Images From a Plane Mirror
We have all used plane mirrors and know the properties of them.
- The image is upright.
- The image is located as far behind the mirror as the object is in front of the mirror.
- The image is the same size as the object.
- The image has left and right reversed.
We can demonstrate this using ray tracing.
Using the similar triangles at the bottom of the figure we see that do = di. We call the
image a virtual image because the light rays do not really come from the image, but we
think that they do. A photographic plate placed at the location of a virtual image will not detect the image because no light rays go through it. However, our eye does see the image
and we could photograph the virtual image or project it on a screen. Just by looking at an image we cannot tell if it is real or virtual.
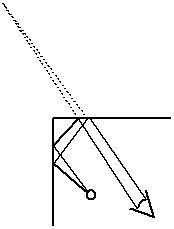
To solve problems in geometric optics, make sure the incident angle is the same as the reflected angle and use geometry.
Problem/demonstration: Mirrors normally reverse left and
right. But if we put two plane mirrors precisely at right angles to each other, they will form an image which is not left right reversed.
We can draw how this works. Something on the left side appears to be coming from the left.
Spherical Mirrors
There are two kinds of spherical mirrors:
- Concave: Reflecting surface is inner surface. Like a cave
- Convex: Reflecting surface is outer surface.
What happens to light rays incident on concave or convex mirrors?
Concave Mirrors
Rays coming from a distant source hit a spherical mirror.
The lines hitting the mirror may be paraxial rays. Paraxial Rays are rays that are close to the principal axis. They are not necessarily parallel to the principal axis. An image is
formed at the focal point for paraxial rays.
The focal point is f=R/2, where R is the radius of curvature of the mirror. So usually a
spherical mirror is small compared to its diameter. A better mirror is actually a parabolic mirror, but harder to make.
We can see where the image is by drawing three rays.
- Ray 1 is parallel to principal axis and goes through the focal point.
- Ray 2 goes through the focal point and bounces back parallel.
- Ray 3 goes through the center of curvature and bounces straight back.
We get different images depending on where the object is relative to C (the radius of curvature) and f (the focal length).
There are three places the object could be.
- Outside of C.
The image is inverted, smaller and real
- Between C and f.
The image is larger, inverted, and real. (It's the same picture as above, but the image just becomes the object.
- Inside of f.
The image is upright, larger, and virtual.
It is nice to draw these pictures, but we need to figure out a quantitative way to solve
these problems. This is analogous to the situation we had with vectors. We could just draw them, but to get a quantitative number we needed a quantitative method, breaking the
vector up into components. So we now develop a quantitative method to do mirrors.
From two similar triangle (all internal angles are the same), we get,
ho/ hi = do/ di ho/hi = (do - f )/f
Set these equal
do/ di= (do - f )/f
Cross multiply and divide both sides by dodif gives
1/ do+ 1/di = 1/f The Mirror Equation
The image is not the same height as the object but has a magnification given by
m = hi/ ho = -di/ do
The Magnification Equations
The minus sign is there because inverted images have a negative magnification. This is very important.
Mirror Sign Conventions:
- 1. Object Distance
- do is + if the object is in front of the mirror (real object)
- do is - if the object is behind the mirror (virtual object)
- 2. Image Distance
- di is + if the image is in front of the mirror (real image)
- di is - if the image is behind the mirror (virtual image)
- 3. Focal Length
- f is + for a concave mirror.
- f is - for a convex mirror.
- 4. Magnification
- m is + for an image that is upright with respect to the object
- m is - for an image that is inverted with respect to the object
 |
 |
|
 PROBLEM
: A clown is using a concave makeup mirror to get ready for a show and is 27 cm in front of the mirror. The image is
65 cm behind the mirror. Find (a) the focal length of the mirror and (b) its magnification. PROBLEM
: A clown is using a concave makeup mirror to get ready for a show and is 27 cm in front of the mirror. The image is
65 cm behind the mirror. Find (a) the focal length of the mirror and (b) its magnification.
This is a virtual image so di = -65
1/27 - 1/65 = 1/f
0.037 - 0.015 = 1/f
0.022 = 1/f Þ f=+46 cm.
m = -(-65)/27 = 2.4
Notice the clown is between the focal point and the mirror.
|
|
|
Demonstration: Use Chalkboard Optics.
Demonstration: Show Mirror Mirage and talk about virtual images.
Convex Mirrors
The mirror equation and the magnification equation hold for convex mirrors as long as
you remember that the focal point has a negative sign. This implies that the image is virtual and upright. (see mirror and magnification equations).
(3rd line not drawn - goes through C and back out, and would intersect with tip of arrow).
 |
 |
|
PROBLEM: The image of a distant
car (passenger side mirror) is located 12 cm behind a convex mirror. What is the radius of curvature of the mirror?
1/ do+ 1/di = 1/f
do = ¥ so 1/do = 0
di = f = -R/2
-12 = -R/2
R = 24 cm
|
|
|
The Refraction of Light
Index of Refraction
In different media, light travels at a different speed than in a vacuum. The speed slows
down, the wavelength decreases but the frequency stays the same in the medium compared to in the vacuum. The ratio of the speed of light in a vacuum to the speed of light in a medium is called the index of refraction (n).
n = c/v
It is always greater than or equal to one. (See chart on page 646). Note how high the index of
refraction is for diamond. This leads to diamonds characteristic sparkle as we shall see.
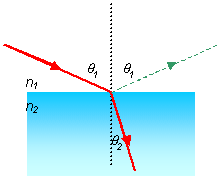 Snell's Law Snell's Law
n1 sin q1 = n2 sin q2
Always use q from the normal
In this diagram n2 > n1
This has lots of consequences.
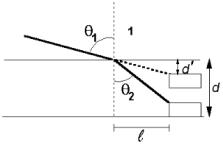 Suppose I am looking at an object that is under water. Light
from the object is refracted at the water, air surface. Suppose I am looking at an object that is under water. Light
from the object is refracted at the water, air surface.
Depth is d. Apparent depth is d¢.
Length along bottom is l.
tanq2 = l/d and tanq1 = l/d¢
We use Snell's law and make the assumption that l is small compared to d (which is the same as saying sinq» tanq for small q ),
n2 sinq2 = n1 sinq1
n2 tanq2 = n1 tanq1
n2l/d = n1 l/d¢
d¢ = d(n1/n2) which is the apparent depth of an object when theobserver isdirectly above it.
 |
 |
|
PROBLEM: An aquarium has a back wall that is 30 cm from the front glass (glass is negligibly
thin). A fish half way between the front and the back is swimming. How close to the front does it appear? (n for water is 1.33)
d¢ = 15.0(1./1.33) = 11.3 cm
If the back wall of the aquarium is a mirror and an image of the fish appears behind
the mirror. How far is this image from the front wall? Image is 15.0 cm behind the mirror
d¢ = 45.0(1./1.33) = 33.8 cm
(Not much further than the back wall). In fact, if n1 is larger, the image could even
appear closer than 30.0 cm.
|
|
|
 |
 |
|
PROBLEM: A submarine is 300 m horizontally from the shore and 100 m beneath the surface. A laser beam is sent from the submarine so that it strikes the surface of the water at a point 210 m from shore. If the beam just strikes the top of a building standing directly at the water's edge, find the height of the building.
n1sinq1 = n2sinq2
1.33(90/{902+1002}1/2) = 1.00(210/{h2+2102}1/2)
{(1.33)(90)} 2/{902+1002} = 2102/{h2+2102}
h2+2102 = 5.57 ´ 104
h2 = 1.16 ´ 104 m2
h = 110 m
|
|
|
Total Internal Reflection
A very important concept. At a certain angle, of reflection, no light will be refracted, but
we will only get reflected light only when the index of refraction of the second media is less than the index of refraction of the 1st media.
sinqC = n2 sin(90°)/n1 sinqC = n2/n1 (n1 >n2).
Fiber optic cables use this idea.
Demonstration: Use Chalkboard optics.
 |
 |
|
PROBLEM: In a fiber optic cable, the index of refraction for the glass is 1.50. What is the smallest angle the
light can get to the parallel direction, and still be totally internally reflected.
(Thisq)
sinqC = n2/n1 ÞqC = sin-1(n2/n1) = sin-1(1.0/1.5) = 42°,
so q = 90°- 42° = 48°
|
|
|
Lenses
Lenses are optical instruments like mirrors. In fact, much of the math we used when
learning about mirrors will be similar here. In the same way we talked about two kinds of spherical mirrors: concave and convex, we will talk about two kinds of lenses, diverging and
converging. We will use equations to determine where real and virtual images will be. We will also look at multiple lenses, and lenses with mirrors. Multiple lenses allow us to
understand a few optical instruments. (Draw Lens and Focal Points).
- Lenses have two focal points, one on each side of the lens.
- Converging lenses are mathematically treated very much like concave mirrors
- Diverging lenses are mathematically treated very much like convex mirrors
- For thin lenses, the thin lens equation and the magnification equation hold.
- Sign conventions are similar to mirrors.
Converging Lenses
- Light converges after exiting the lens.
- Thicker in the middle than at the edges.
Use three rays to see where image is:
- Parallel and through the far f.
- Through the near f and exit parallel.
- Through the center and straight.
Like concave mirrors, the image formed depends on where the object is located with respect to the focal length.
- Farther than 2F, the image is real, inverted and smaller.
- Between 2F and F, the image is real, inverted and larger.
- Closer than F, the image is virtual, upright, and larger.
For thin lenses (the lens is thin compared to f, so we can measure from anywhere on the
lens), the thin lens equation and the magnification equations hold.
1/do + 1/di = 1/f
m = hi/ho = - di/do
Lens Sign Conventions:
- Object Distance
- do is + (real) if the object is on the same side of the lens as the original object
- do is - (virtual) if the object is on the opposite side of the lens from the original object
- Image Distance
- di is the same sign as that of the object if the image is formed on the opposite side of the lens from the object.
- di is the opposite sign as that of the object if the image is formed on the same side of the lens as the object.
- (So if the object is + (real) an image formed on the opposite side of the lens as the object will be + (real), and an image formed on the same side of the lens as the object will be - (virtual).)
- Focal Length
- f is + for a converging lens.
- f is - for a diverging lens.
- Magnification
- m is + for an image that is upright with respect to the object
- m is - for an image that is inverted with respect to the object
 |
 |
|
 PROBLEM
: The movie film in a theater has a width of 70 mm.
The projector lens has a focal length of 305 mm. If the screen in the theater is 60 m from the projector, how wide is the image. PROBLEM
: The movie film in a theater has a width of 70 mm.
The projector lens has a focal length of 305 mm. If the screen in the theater is 60 m from the projector, how wide is the image.
1/do + 1/60 = 1/.305
1/do = 3.28 - .02 = 3.26
do = .307 m
m = hi/.070 = - 60/.307
hi = -13.7 meters (negative sign means inverted)
|
|
|
Diverging Lenses
- Light diverges after exiting the lens.
- The lens is thinner in the middle than at the edges.
We use three rays to see where the image will be focused.
- Incident parallel and exits in a direction that appears to have originated from the first f.
- Is incident on the second f and exits parallel to the principal axis.
- Goes straight through the middle.
Like a convex mirror, a diverging lens only has one possible image that can form,
independent of the location of the object. A diverging lens always forms an image that is virtual, upright, and smaller than the object. Use the same thin lens equation with the
appropriate signs, and the same magnification equation.
Lenses in Combination
Most optical images use lenses in combination. The image from one lens serves as the
object of the other lens. To do a problem, you have to do two separate problems: solve for
the first image - then use that as the object to solve for the second image. Let's see how this works.
 |
 |
|
PROBLEM: Two converging lenses are placed 20.0 cm apart. If the first lens has a focal length of 10.0 cm and
the second lens has a focal length of 20.0 cm, locate the final image of an object located 30.0 cm in front of the first lens.
For the first lens I do the problem as if the second lens did not exist.
1/30.0 + 1/di= 1/10.0 Þdi= 15.0cm
So the image is 15 cm from the first lens, which means it is 5.0 cm from the second
lens. So for the second lens, the object distance is now 5.0 cm.
1/5.0 + 1/di= 1/20.0 Þdi= -6.7cm
So the final image is 6.7 cm to the left of the second lens.
What is the magnification of the two lenses?
The magnification from the first lens is M1 = -di/do = -15/30 = -1/2
From the second lens M2 = -di/do = 6.7/5 =1.3
so the total magnification is
M = M1M2 = (-1/2)(1.3) = -0.67
|
|
|
 If I add mirrors in combination with lenses, the method is the same. The image from the first element (mirror or lens)
becomes the object for the second element. If I add mirrors in combination with lenses, the method is the same. The image from the first element (mirror or lens)
becomes the object for the second element.
|