Chapter 24 Lecture Notes

Formulas:

Double slit diffraction: 

Bright fringes when       sinq = ml/d                   m = 0,1,2,...
Dark fringes when         sinq = (m+1/2)l/d         m = 0,1,2,...

Single slit diffraction     sinq = l/W            for first dark fringe

Bright spots in diff. grating      sinq= ml/d       m = 0,1,2,... 

Thin Films:            (NPC º Net Phase Change)

2t = ml_film            

Constructive interference when NPC = 0
Destructive interference when NPC = 1/2l_film

2t = (m +1/2)l_film 

Destructive interference when NPC = 0
Constructive interference when NPC =1/2l_film

S = S_ocos²q         

tanq_B = n₂/n₁                            

Demonstrations:

• Lasers and diffraction
• Single slit white light diffraction grating to give colors. 

Dispersion: Rainbows and Prisms

     Dispersion occurs because the index of refraction depends on the wavelength of the light.  White light is made up of colors from the entire spectrum.  The spectrum is ROYGBIV (red, orange, yellow, green, blue, indigo, violet).  In a prism, violet light has a larger index of refraction than red light, so it is diffracted more.  This is called dispersion.  Up until now, we have been treating the index of refraction as being independent of wavelength, but it is really not. Dispersion is responsible for splitting white light into different colors in a rainbow, or from a prism.

Red - Violet (n for violet is greater thann for red). 

     We see a rainbow due to dispersion. Light from the sun (behind you) reflects off of water drops like in the figure.  Violet is diffracted more than red, so you see the violet part of the rainbow lower than the red part. We see red when we look up high, and violet when we look down low.  (This is figure 24-13 in the book)

The Wave Nature of Light

Introduction: Waves and Particles

     Waves and particles behave differently.  Geometric optics primarily looks at light as a particle.  In this chapter we will talk about the wave nature of light. Waves that are directed exactly perpendicular to a slit will diffract, or change direction at the slit. However, particles entering perpendicular will either go straight through or they bounce back.  We find that light will diffract and behave like a wave.  What about geometric optics? It only works when the wavelength of light is small compared to the geometry involved.  When the size of the wavelength is comparable to the size of the physical objects involved, then light will exhibit wave-like properties.  

     What happens when a wave or a particle goes through two slits? A particle must go through either slit but a wave goes through both and produces an interference pattern. 

     However, there are cases when I can make light behave like a particle even when the geometry is small.  In fact, I can show light to be both a wave and a particle.  We will talk more about that in chapter 27.  However, now we will focus only on the wave nature of light. (electro-magnetic radiation). 

Huygen's Principle

     Christian Huygen's principle predicts where the wavefront will be at a later time. It says that every point on a wavefront can be considered as a source for more wavefronts.  The new wave will be tangent to all the little wave fronts. (See figure 24-1, and 24-2). This can be used to explain what happens when light encounters a slit.

The Principle of Superposition

     You must understand this principle to understand chapter 24.  When two waves are in the same region of space, the amplitude of the produced wave is just the sum of the amplitudes of the two waves.  Therefore, waves can exhibit constructive or destructive interference.  We talked about this in chapter 11.

Constructive Interference

Light is a wave and waves have peaks and valleys.  If peaks from two waves align, the E and B fields are added and the intensity increases. This is constructive interference. The waves are in phase. The light is brighter.

Destructive Interference

If a peak lines up with a valley, then the E and B field cancel and we have destructive interference. The intensity is 0.  The waves are 90° out of phase.  There will be no light.

Coherent Sources

Light will only demonstrate noticeable interference effects if it is coherent light. Two waves of light are from a coherent source if the phase relationship between the waves does not change. That is the two light rays always have their peaks and valleys in the same phase relative to each other.  If the relative phases stay the same as time passes, then the constructive or destructive interference remains.  In order to do this, the different waves must have the same velocity, wavelength, and frequency.  Lasers are coherent sources of light, while light bulbs and fluorescent lamps are incoherent sources.  That is why we don't normally see interference effects from normal light sources.

Applications of the Principle of Superposition

Remember that for small angles sinq»q when q is expressed in radians. C= pd = 2pr.  So we see that an arc length a = qr in radians.  Therefore,               q = a/r»d/r = sinq )

Young's Double Slit Experiment

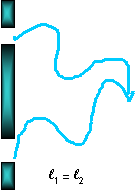     If light from a coherent source is incident on two slits, we may get constructive interference or destructive interference depending on the difference in the distance that the light has to travel. Thomas Young used this idea to demonstrate that light was actually a wave, since particles will not demonstrate constructive and destructive interference.  Suppose the light from one slit travels a distance l₁ and the light from the other slit travels a distance l₂. 

There will be constructive interference, (or a bright spot) where l₂ = l₁ + l.  For instance when l₁ = l₂ (at the center) there will be a bright spot.  If the difference between the two distance is one half a wavelength, there will be destructive interference, (a dark spot) when             l₂ = l₁ + l/2.

 Another picture:

     Now we draw the situation in more detail and do calculations.   When the screen is far compared to the slit distance, the waves are approximately parallel and all angles q are the same.

When D l is equal to one wavelength, the light is constructive and bright.  When it is one half wavelength, the band is destructive and dark. 

So Bright fringes when         sinq = ml/d                   for m = 0,1,2,...

Dark fringes when                    sinq = (m+1/2)l/d            for m = 0,1,2,... 

The fringes are called higher order maximums (1st order, 2nd order, etc.)

Problem/Demonstration: Determine the wavelength of laser from double slit diffraction pattern using the distance between the zeroth order bright spot and the first order bright spot. sinq = lm/d sinq = x/(x2+l2)1/2   l = dx/m(x2+L2)1/2  Suppose we are a distance of 20.0 m from the screen and the distance between the slits is .250 mm.  We measure the distance between the zeroth order maximum and the first order maximum to be 0.0500 meters.  What is the wavelength of the light? Using the above equation with m=1 gives   l=6.25´10-7 m = 625 nm

Single Slit Diffraction

     We talked about Huygen's Principle before.  This can lead to diffraction patterns from a single slit if the wavelength of light is approximately the same size (or larger) than the size of the slit.  The size is important for diffraction because if the wavelength is much smaller than the geometry we will not see wave-type phenomena.  That is why we don't see diffraction patterns around doors.  Also, coherence is important for creating visible diffraction patterns.  (Most natural light is incoherent).  Diffraction occurs even if the light is incoherent, but diffraction patterns aren't seen. 

Bottom cancels out the top and so the first dark fringes are at  

sinq = ml/W

  

Problem/Demonstration: We have determined the wavelength of the laser.  If we now know the distance to screen, L, and slit width, W, what will the distance between the first two dark fringes?  sinq = y/(y2+L2)1/2 = l/W            where y is the distance between the                                                          dark fringes divided by two.  With W = .0200 mm, and l = 625 nm and L = 20 m, we solve for y.   Because y is small compared to L, we can say that y2+L2 = L2.    So  y = lL/W = 62.5 cm.  So the width of the central maximum is 125 cm.  Illustration:  If you don't have your glasses on and you make a small hole with your fingers, why does this work?  (Diffraction like a diverging lens).  Because the angle of diffraction depends on the wavelength, we can use a slit to separate the colors in white light.

Demonstration:  Single slit diffraction grating using white light to give colors. 

Diffraction Grating

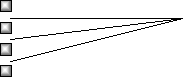     Diffraction gratings put many slits in a row.  The bright spots occur at the same location as for a double slit experiment.  

First one travels an extra l, the second one and extra 2l, etc. 

They are at sinq= ml/d   for m = 0,1,2,... 

However, the peaks are much sharper and narrower on a diffraction grating.   For two slits when you move slightly off the maximum, you are just slightly out of phase.  When there are multiple slits, and you move off slightly.  The light from a distant slit is already out of phase and you get a dark spot. 

     Consider the case where I have 100 slits and I move a distance that is 1/100l away from the peak.  If I had only two slits the phase difference is only 1/100 l, so things don't change much because the change is only 1(l + l/100) = 1.01l. However, if I have 100 slits the extra distance from the 50th slit away is 50(l + l/100) = 50.5l which is one half wavelength.   So slit 1 cancels slit 51, etc.

PROBLEM:  A diffraction grating contains 4820 lines/cm and is used with blue light (l = 470 nm). What is the highest order bright fringe that can be seen with this grating?  sinq = ml/d                 The maximum sinq  can be is 1, so  1 = ml/d  m = d/l = 1/(4820 lines/cm)(100 cm/m)(470nm)(1´10-9 m/nm) = 4.4    So the maximum is 4th order fringe.

Thin Film Interference

     Thin film interference will occur because the distance traveled by the light reflected off the gas is different than the distance traveled by the light reflected off the water. 

The wavelength that matters is the wavelength of light in the gas since that is where the difference occurs. 

n = c/v = (c/f )/(v/f ) =l_vacuum/l_film

l_film = l_vacuum/n 

So you would think that we get constructive interference when:

2t = ml_film = ml_vacuum /n. 

By this is not quite right because when light is reflected from an object with a larger index of refraction, the wavelength changes by l/2.   Remember the rope analogy from chapter 11, figure 11-25.  We get a net phase change of 1/2l when going from a medium with a lower index of refraction to a medium with a higher index of refraction.  We do not get this phase change when going from an index with a higher index of refraction to one with a lower index of refraction. 

First do this attached to wall and loop, then attached to heavy and light strings. Some goes forward and some is reflected. 

So we get constructive interference when  

2t = (m+1/2)l_film =(m+1/2)l_vacuum /n. 

Destructive interference would be when 2t = ml_film = ml_vacuum /n. 

So we see that if the net phase change (NPC) is 1/2l_film, then we get

2t = ml_film             Destructive interference

2t = (m +1/2)l_film  Constructive interference         

What if the media bottom was not water, but glass with n=1.52.  Then there is also a phase change at the gas, glass boundary, and no net phase change.  

We find that for no NPC, we get  

2t = ml_film             Constructive interference

2t = (m +1/2)l_film  Destructive interference         

Destructive interference will look dark.  Just before the bubble breaks, the thickness will be 0, and the 1/2 phase difference will cause destructive interference, and the bubble will look dark at its weakest point. 

Cancellation of a color occurs when there is destructive interference.  Something looks a certain color when there is constructive interference. 

     On many cameras and fine quality lenses, the manufacturer will try to eliminate reflection of the light.  To do this, they make a compound lens which are lenses made from a number of different types of glass.  For instance, if I coat glass with magnesium fluoride the reflection from the surface can destructively interfere, and I will get no reflected light of a certain wavelength. MgF₂ has n» 1.38 and glass has n» 1.5.

PROBLEM: A non-reflective coating of magnesium fluoride covers the glass of a camera lens.  Assuming the coating prevents light of 565 nm from reflecting, what is the minimum thickness of the coating?  lfilm = lvacuum/n = 565nm/1.38 = 409 nm  There is no net phase change (because there is a phase change of 1/2 l  at each surface), so I get destructive interference when  2t = (m +1/2)lfilm t = 1/4lfilm = (1/4)409 nm = 102 nm.

An Air Wedge

     An air wedge also uses this same principle as thin film interference to see if a surface is completely flat.

If it is flat, then the wavelength difference will be because of the geometry and diffraction patterns will be regular.  If it is not flat, then the diffraction patterns will not be regular  (see figure 24-27) 

Where will the phase of the reflected ray change by 1/2?  (At the first glass to air boundary).  What will the fringe look like where the plates touch?  (It will be dark because of the 1/2 l change.) 

Polarized EM Waves

     Because light is a transverse wave, it can be polarized.  Normal light has the direction of its electric field randomized in space.  A polarizer only allows the electric field going in one direction to pass through. 

     The size of slit depends on wavelength of object.  For instance, a microwave grid stops microwaves but not visible light. A cooling tray will actually polarize microwaves.

     What happens to the intensity of the beam?  If I allow un-polarized light to go through a polarizer, I find that the intensity of the polarized light is cut by 1/2. 

When I add another polarizer, the change in intensity depends on the angle of the second polarizer and is given by

S = S_ocos²q           (Malus' Law) - When q is 90°, no light passes through. 

What happens if I put a third polarizer in? 

S₁ = (1/2)S_o

S₂ = S₁cos²q₁

S₃ = S₂cos²q₂

S₃ = S₁cos²q₁cos²q₂ = (1/2)S_ocos²q₁cos²q₂

The polarizer is actually picking out the component of the electric field which is parallel to the axis of polarization. 

Demonstration/Problem:  Polarized light. 

If I have two polarizers at 90° with respect to each other, then no light will get through because S₂ = S₁cos²q₁ = S₁cos²(90) = 0. 

However, if I put a polarizer between them at an angle of 45° with respect to the two polarizers, I will find, 

S₃ = (1/2)S_ocos²(45^o)cos²(45^o) = .125S_o  so some of the light gets through. 

Light will get through as long as one of the polarizers is not at 90° to the one directly in front of it.

Polarization by Reflection

     When light is reflected off of a surface it is also polarized.  Any light reflected off of a surface will be partially polarized along the horizontal direction.  Polaroid sunglasses have their axis of polarization along the vertical direction to stop glare from reflected light which is always partially polarized along the horizontal direction. At a certain angle the reflected light will actually be totally polarized.  This angle is called Brewster's angle and it is given when 

tanq_B = n₂ /n₁

 The book shows that at this angle, the angle between the reflected and the refracted rays is 90°.