Two-Dimensional Cellular Automata
A two-dimensional cellular automata consists of a grid of cells rather than a row of cells.
As in the one-dimensional case, the cells also have values from a finite alphabet and a local rule to update
those values. In the one-dimensional case the local neighborhood which determines the cell's next value
consisted of the cell itself and its neighbors to the left and to the right. Two-dimensional automata have neighbors in more directions.
The most well known example of a two-dimensional cellular automata is John Conway's Game of Life. (A web search on "Game of Life"
will turn up numerous references, probably including programs you can download to experiment with the automata. We include one such site
available as of 10/02, in our list of
references.)
Two popular ways of specifying a cell's neighborhood are displayed below. In one the neigborhood consists of nine cells, and
in the other the neigborhood
consists of only five. Consider the three-by-three grid in the figure below. In a nine-point rule all the cells in this
grid would be considered neighbors of the center cell. In a five-point rule, only those which share an edge with the center
cell would be included. Thus the four corners, although diagonally adjacent to the center cell, are not available to the rule.
| 9
point only |
5 and
9 point |
9
point only |
| 5 and
9 point |
5 and
9 point |
5 and
9 point |
| 9
point only |
5 and
9 point |
9
point only |
The same kinds of questions arise for two-dimensional cellular automata as arise for one-dimensional automata.
As in the one-dimensional case, if we use a finite grid, there are only finitely many possible states, one of which is the
state where all
cells have the value of zero, or the identity. If this state is reached, the cellular automata continues in this state
forever.
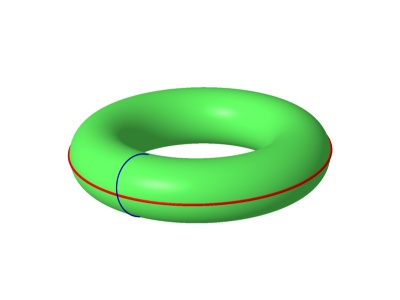Since there is really no action at this point, we generally refer to this state as "death"; we say
a cellular automata initial state that eventually reaches this state "dies" or "dies out." As we did in our example in the one-dimensional case, we
define the cells at the righthand edge of the grid and the cells at the lefthand edge to be next-door neighbors. We also define the
downstairs neighbors of the bottom row to be the first row and the upstairs neighbors of the first row to be the last row. In this manner we are really
wrapping our rectangle into the surface of a donut shape or a torus.
Attached are some examples of group multiplication rule cellular automata.
These were created using a five-point rule of clockwise group
multiplication not including the center. This file has
some large animated .gif files and may take a while to load. Click on any one to view an enlarged version.
If you are having trouble loading or running these animations, you might want to try our
supercompressed versions instead.
We also include some examples of nine-point rule automata. This file also has large .gif files and may take a while to load.
If you are having trouble loading or running these animations, you might want to try our
supercompressed versions instead.
Andy's Applet's:
Would you like to run your own two-dimensional automata?
