One-Dimensional Cellular Automata
A one-dimensional cellular automata is simply a row of cells, each of which has some value from a finite
alphabet, together with a local rule for changing the values of the cells in discrete time steps. A configuration where each cell has a specific value from the alphabet
is called a state. The local rule,
called the update rule, assigns a new value to a cell based on its current value and the values of its neighbor cells.
For example, Pascal's Triangles mod n or the PascGalois Triangles discussed in section 2 can be viewed as one-dimensional cellular automata with an infinite number of cells.
Just consider each row of the triangle as extending indefinitely in either direction. Each entry of the triangle corresponds to a cell and its value.
We can just consider the "hidden" cells outside the triangle as having values of zero or the identity.
Then you can update the automata
by combining the current value of a cell with the current value of the cell directly to the right of it.
Then place the row of cells with new values directly below the old row. You get the PascGalois triangle skewed to the
right. For example, here are two versions of the first 125 rows of Pascal's Triangle
mod 5 (or the PascGalois triangle for Z5):

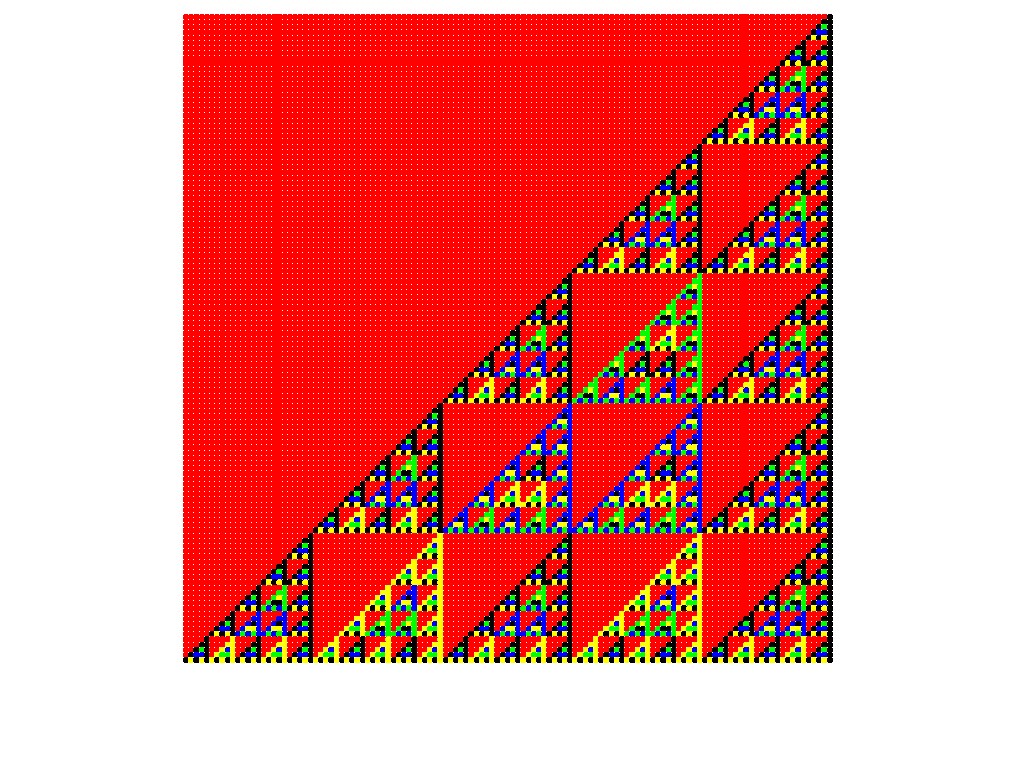
This is an example of an infinite cellular automata. Remember that each row of these picures represents a different state of the automata, so that as you move down the
rows, you are moving through the temporal evolution of the automata. Of course, for this to generalize to PascGalois triangles with two different values down the
two sides, we have to begin with a row with two non-identity entries. With Pascal's Tirangle mod n, we can begin with the top row with a single
entry of one.
We can also define related finite cellular automata by either fixing the values of the cells on the ends or
by wrapping the cellular automata around so that you define the cell on the right of the last cell to be your first cell
and the cell on the left of your first cell to be the last cell. Essentially, you define your automata as if the row of cells is in fact a circle of
cells. You can then apply the same update rule. Suppose we do the mod 5 example again with 25 cells wrapped
into a circle and display them as above: -

Notice that the values begin to repeat, i.e. the last 25 rows look just like the first 25. In fact, this particular cellular automata
repeats every 100 rows. Since we have only finitely many cells and only finitely many values they can take on, the cellular automata has finitely many possible states,
so eventually, it has to repeat a state it has already taken on. Once it does that, the subsequent states will also repeat.
With finite cellular automata, no matter what state you begin with, you always evolve to a repeating cycle eventually. This repeating cycle is called a periodic cycle. The
sequence of states taken on before reaching the periodic cycle are called transient states. For our example, since the
entire set of states repeats, there is no transient.
If we try this with 18 cells instead of 25, the periodic cycle contains 2232 states and the initial state, the one with only one non-zero value, does not repeat;
it is transient. What is it that makes this different? Can we predict in advance what the length of the periodic cycle will be?
Does it change if we begin with a different initial state or does it depend only on the number of cells we're using?
If we use some other group multiplication rather than Z5, how will that change things? It is relatively easy to play around with examples of these and to make conjectures about them,
but proving them is another matter. Besides looking at other groups, we can look at other update rules.
For example, you might define the new value of a cell to be the sum of or the product (using group multiplication) of the value of the cell to the left and the value of the cell to the right.
Our undergraduate research students have been able to answer some of the questions that arise in these investigations (see, for example, [10] and [12]) for some examples
but there are still many questions left to explore.
Another way to generalize this idea is to consider two-dimensional cellular automata.






