PascGalois Triangles for some of the Dihedral Groups
 |
 |
 |
| D3 PascGalois Triangle |
D4 PascGalois Triangle |
D5 PascGalois Triangle |
 |
 |
 |
| D6 PascGalois Triangle |
D7 PascGalois Triangle |
D8 PascGalois Triangle |
All of these triangles were produced by placing a rotation though 360/n degrees down the right side of the triangle and
a flip down the left. It is left as an exercise for the reader to verify that repeated multiplication of these two elements will
generate the entire group for all n. This is the standard construction we will use for PascGalois Triangles for
Dn throughout this paper.
Would you like to see them in different colors?

You may notice that D4 and D8 have much more easily discernable patterns than the others.
Unfortunately, the reason for this is beyond the scope of this paper. However, if we change the coloring scheme so that all the rotations are
colored blue/green and the flips are colored red/purple, see what happens:
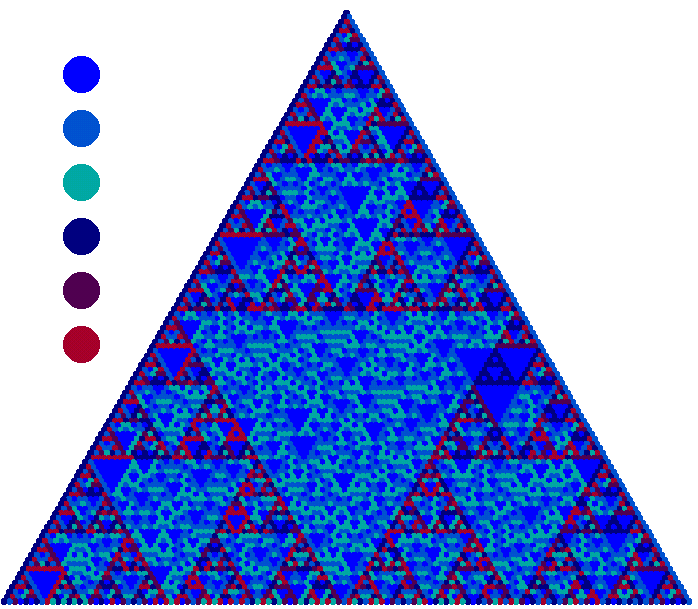 |
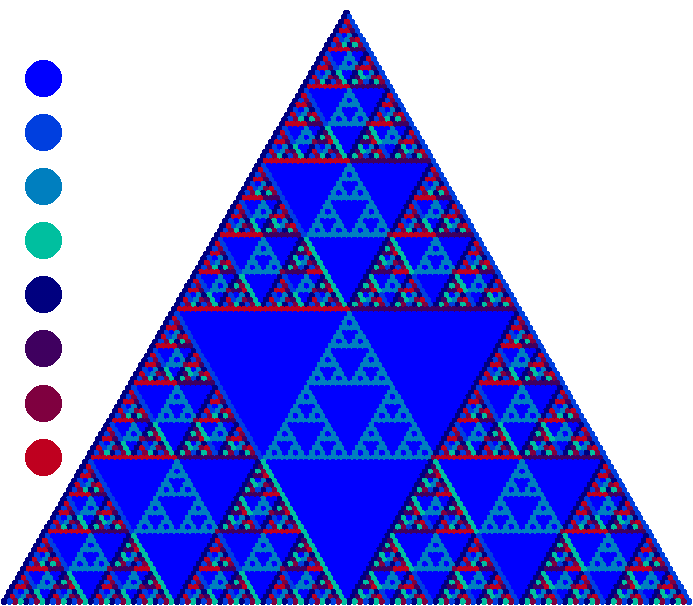 |
 |
| D3 PascGalois Triangle |
D4 PascGalois Triangle |
D5 PascGalois Triangle |
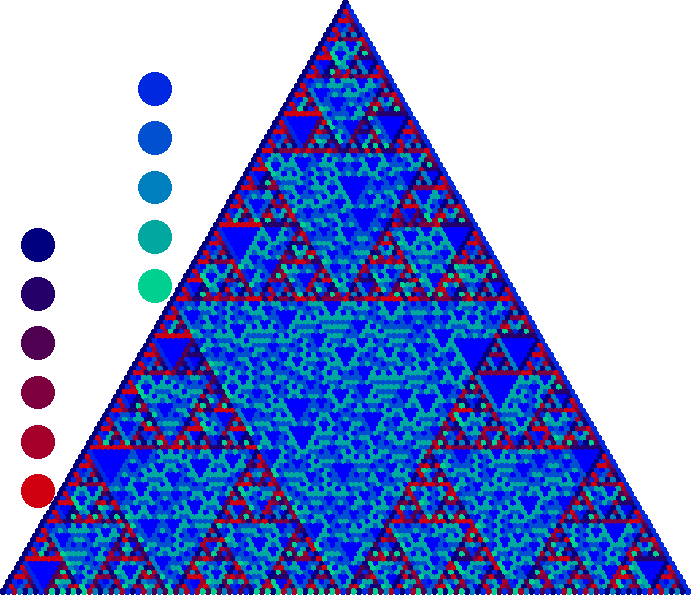 |
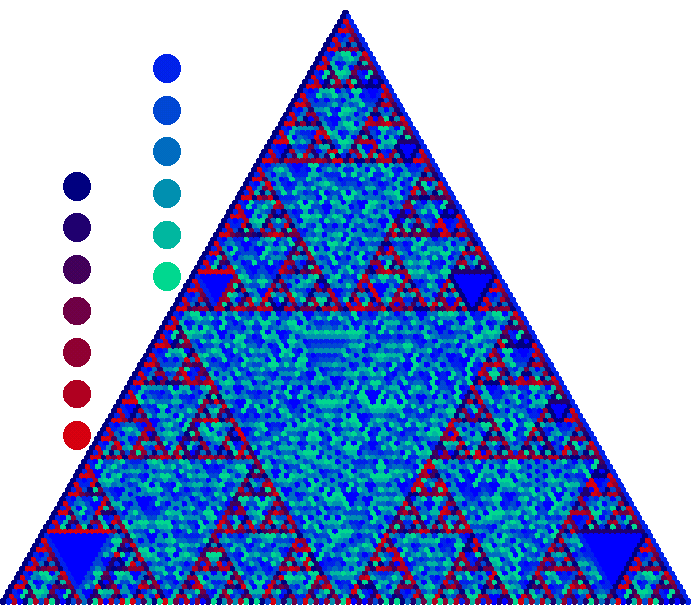 |
 |
| D6 PascGalois Triangle |
D7 PascGalois Triangle |
D8 PascGalois Triangle |
Although the triangles for some are always fuzzier than others (e.g. D4 and D8), all
of the triangles exhibit the similarity to the triangle for Z2 when rotations and flips are clearly distinguishable.
Again, this happens because when you lump all the flips together as if they were the same element and you lump the reflections
together as if they were all the same, the resulting multiplication table is the same as that for Z2 with 0 replaced by
the rotations and 1 replaced by the flips.






















