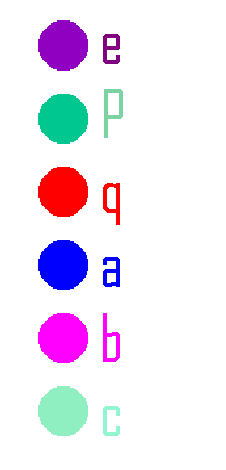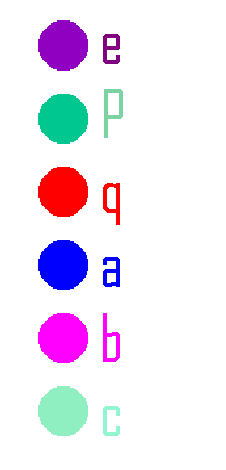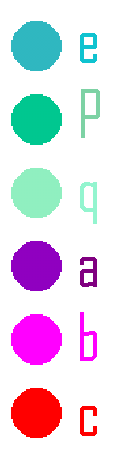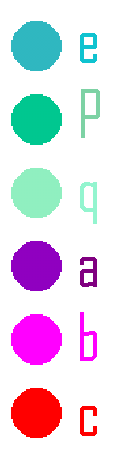PascGalois Triangles for D3, the Symmetry Group for an Equliateral Triangle.

As was the case with Z2 x Z2, there is no single element that can generate all of D3. However, a (or any one of the flips) together with any second element other than e will generate it, so we can still construct PascGalois triangles that display all of the group elements eventually. We chose to put a rotation, p, down the right side of the triangle and a flip, a, down the left side. Here is what you get with the first 66 rows:

Nothing seems to jump right out as a pattern here, let's see what a few more rows might do:
It is still difficult to discern a pattern. How about if we start shifting colors around? Let's swap the colors for p and c:

That is a little better. How about if we swap the colors for a and e now:

Now, what if we moved the blue color over in the spectrum towards green a little:

Remember what the PascGalois Triangle for Z2 looked like? Lets redraw it using green for 0 and purple for 1:

Putting these together, we see that the only difference, aside from the variation in colors in the D3 triangle, is the extra row of green along the right hand edge. This occurs because we are using two generators for the D3 triangle. If we were to start the Z2 triangle with 1's down the left edge and 0's down the right, the result would be essentially the same as the D3 triangle with e, p and q green and a, b, and c purple:

Why is this? Consider e, p, and q as rotations, and relabel them all r. Consider a,b, and c as flips and relabel them all as f. Remember the multiplication table for D3:
* e p q a b c
e e p q a b c
p p q e b c a
q q e q c a b
a a c b e q p
b b a c p e q
c c b a q p e
Notice that a flip times a flip is always a rotation while a rotation times a rotation is a rotation, and a flip times a rotation or a rotation times a flip gives a flip. So identifying all the rotations and all the flips gives:
* r f
r r f
f f r
But the multiplication table for Z2 is:
* 0 1
0 0 1
1 1 0
So they are essentially the same or isomorphic.
Click next to continue on to see PascGalois triangles for other dihedral groups. If you have not read about these groups yet you may wish to do so now.