PascGalois Triangles

Let us see what happens when we make a PascGalois triangle using the group Z2xZ2 Remember that the multiplication table for this group is:
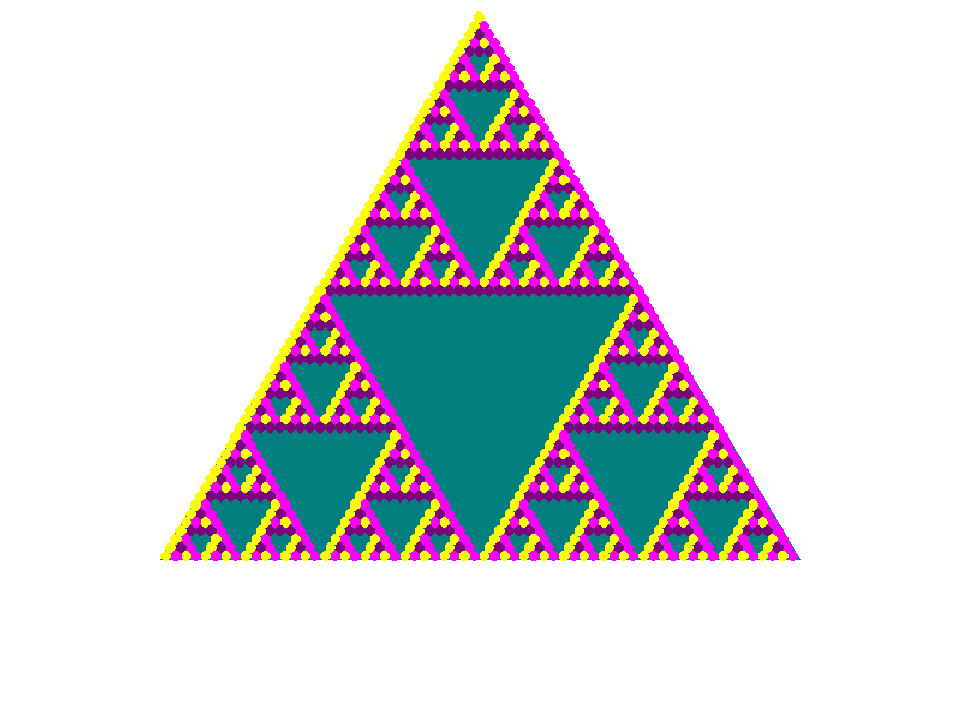
* (0,0) (0,1) (1,0) (1,1)
(0,0) (0,0) (0,1) (1,0) (1,1)
(0,1) (0,1) (0,0) (1,1) (1,0)
(1,0) (1,0) (1,1) (0,0) (0,1)
(1,1) (1,1) (1,0) (0,1) (0,0)

Now we have to choose which elements to place down the sides of our triangle. Notice that if we chose to place (0,1) down both sides, combining (0,1) with itself gives (0,0) and combining again with (0,1) gives (0,1) again so the element (0,1) can not generate the whole group. Note that, unlike the case of modular addition where repeated addition of ones will generate all of the possible results, in this set there is no single element that generates the whole set. Thus we decided to put the element (1,0) down one side of the triangle and the element (0,1) down the other side. In this triangle, the pink is (0,1), the yellow is (1,0), the purple is (1,1), and the teal is (0,0).

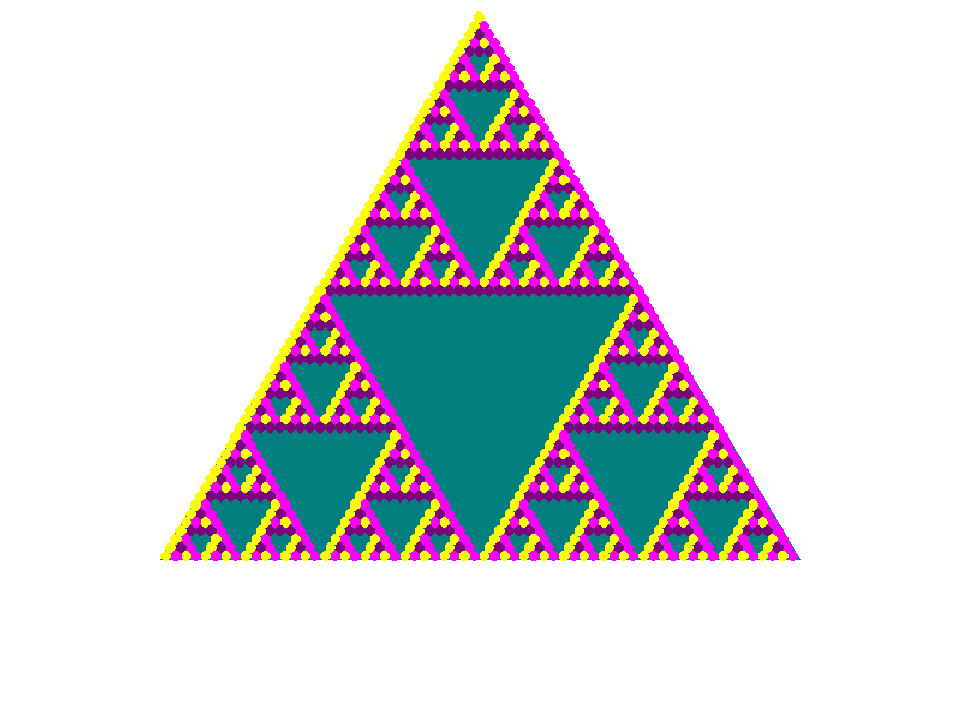
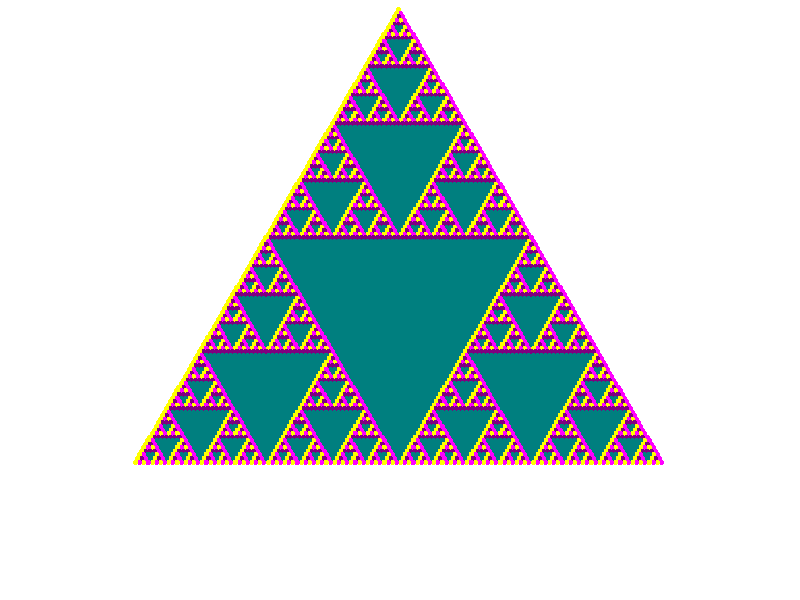
If you would like to see a few more rows . . .

Does this triangle remind you of any of the modular arithmetic triangles? In particular does it remind you of the mod 2 triangle also known as the Z2 PascGalois triangle? Let's look at the Z2xZ2 triangles with 50 rows again. Below we begin to change slowly the color corresponding to (1,1) to the color corresponding to (0,0). Then we change the color corresponding to (1,0) until it matches the color corresponding to (0,1). The final triangle is the Z2 triangle redrawn using teal for zero and pink for one. The colors corresponding to the different elements are displayed in order {(0,0),(0,1),(1,0),(1,1)} to the left of each triangle.

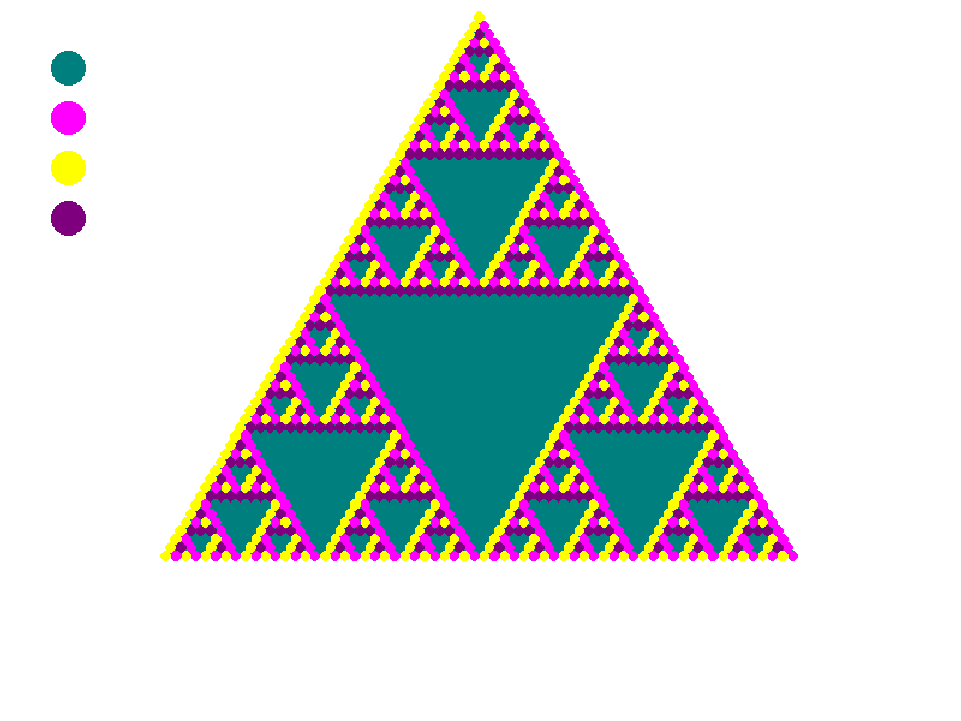Z2xZ2 PascGalois triangle with teal identity Z2xZ2 PascGalois triangle with teal identity and (1,1) moving to teal Z2xZ2 PascGalois triangle with teal identity and (1,1)moving to teal Z2xZ2 PascGalois triangle with teal (1,1) and identity
Z2xZ2 PascGalois triangle with teal (1,1) and identity and (1,0) moving to pink Z2xZ2 PascGalois triangle with teal (1,1) and identity and (1,0) moving to pink Z2xZ2 PascGalois triangle with teal (1,1) and identity and (1,0) moving to pink Z2 PascGalois triangle with teal identity and 1 in pink
Below is an animation showing the same identification occurring in the 128 row triangles.

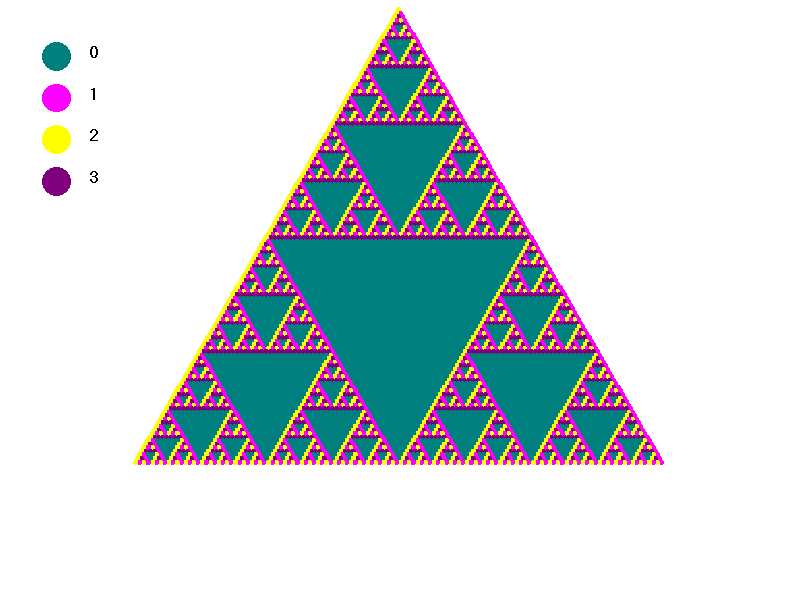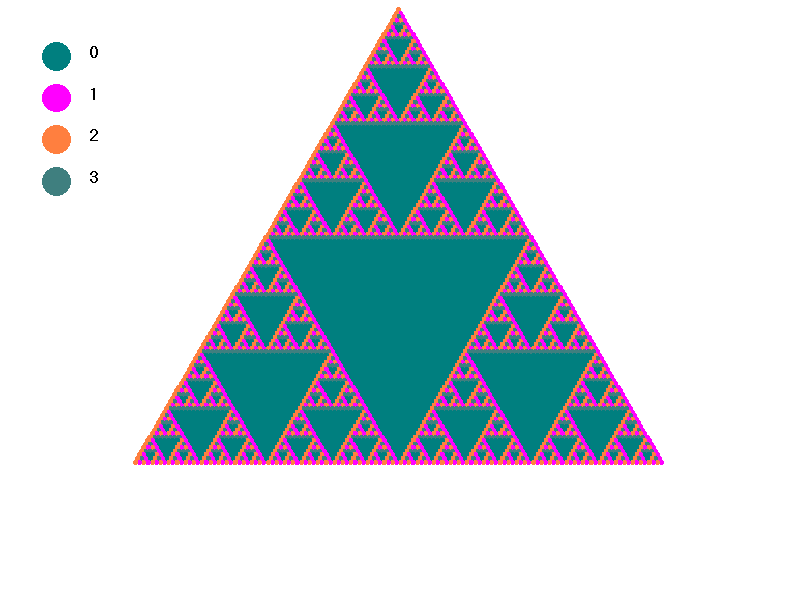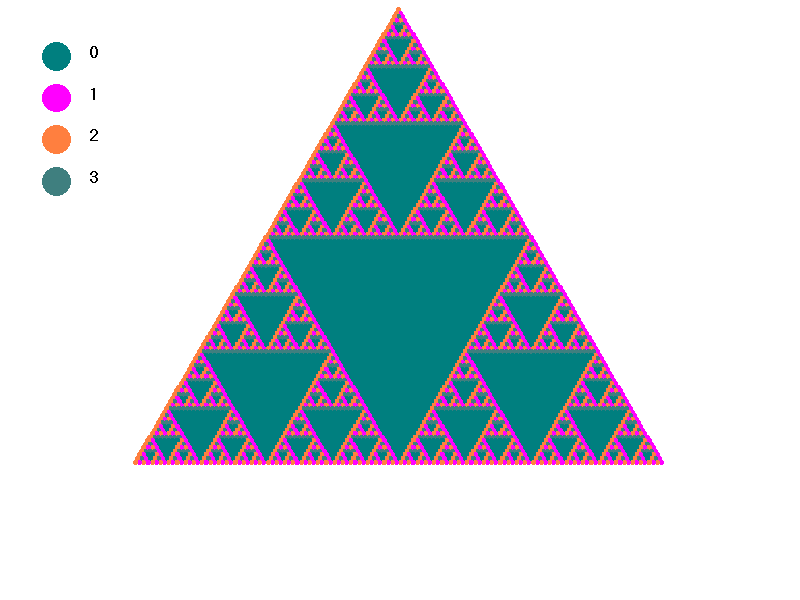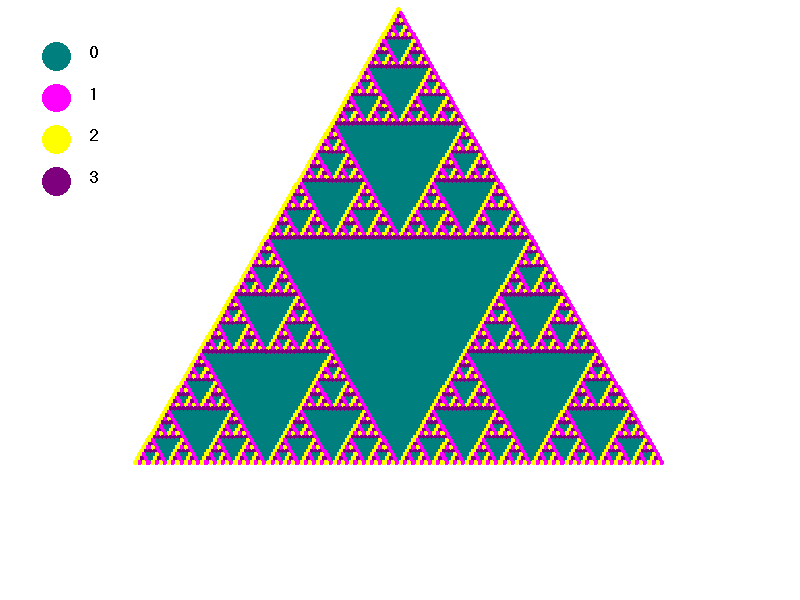
Next we can look at another example. If you did not already read the explanations of the symmetry groups, you might wish to do so now . Otherwise you can proceed to look at their PascGalois triangles.