MATH 230 Fundamental Concepts II
Fall 2009 Assignments and Tests

 

View the "Guidelines for Written Work."

Each assignment you submit must be enclosed in a cover sheet employing a prescribed format. Information on "The Prescribed Format for Assignment Cover Sheets" can be found by following the link below. Submit written solutions for the exercises in parentheses and any other exercises where you are instructed to provide a written solution.  You should do the other exercises for practice or self-testing. Up to the due date for the assignment, for optional credit you are invited to place solutions to exercises identified with an asterisk (*) on the board prior to class.  Write up your problem solutions so that your paper is easy to read and your method and thought process are clear to the reader. Carefully state your conclusions in the form of complete English sentences.  All assignments are due at the beginning of the class period on the assigned due date.  No late papers will be accepted.

 

The Prescribed Format for Assignment Cover Sheets

 

Go directly to:

 

Assignment #1 - Due on Wednesday, Sept. 9 (Section 002) and On Tuesday, Sept. 8 (Section 004)

 

1.)  If you have not already done so, activate your computer account.

 

2.)  Log in on the campus computer system and do the following:

a) Read any incoming e-mail from your instructor you find in your mail box.
b) Send an e-mail message to your instructor.  If you choose to use an e-mail account other than your SU GroupWise account, you may do so.  However, you must arrange to have your e-mail to your campus account forwarded to your preferred account. "Speedy Sheets" with instructions for using GroupWise can be found at http://helpdesk.salisbury.edu/informationCenter/documentation/speedysheets/speedysheets.htm#GroupWise.


3.)  Access the home page for this course.  (http://faculty.salisbury.edu/~dccathcart/Math230/Math230Home.html)


4.)  Follow the appropriate links and read the letter "To the Student, the "Course Syllabus," your "Instructor's Policies," and the "Guidelines for Written Work."

 

5.)  Read the indicated sections in your text and work the exercises indicated below.  Turn in written solutions only for the exercises whose numbers are enclosed in parentheses or where your are specifically asked to write up a solution.  Up to the due date for the assignment, for optional credit you are invited to place solutions to exercises identified with an asterisk on the board prior to class.  Write up your problem solutions so that your paper is easy to read and you method and thought process are clear to the reader. Carefully state your conclusions in the form of complete English sentences. When you submit your paper, be sure it is enclosed in a cover sheet employing the prescribed format. All assignments are due at the beginning of the class period on the assigned due date.  No late papers will be accepted.

 

Read, and work through, Sections 6.1-6.3 in the text.  It is assumed that you already have mastered the skills and concepts addressed in those sections.  So, most of that material will not be presented in class.  It will be your responsibility to ask questions in class about any material in those sections that you find confusing.  Turn in written solutions only for the "regular exercises" and "problem solving exercises" whose numbers are enclosed in parentheses.  Write up your regular exercise solutions in a step-by-step manner so your thought process is clear.  (Regular exercises are not designated by the "PS" icon.)  Write up your problem solving exercise solutions employing Polya's four-step process demonstrated in the problem problem solutions on p. 381 and on p. 405-6.)  Problem solving exercises are designated by the "PS" icon.)  Up to and including the due date for the assignment, for optional credit you are invited to place solutions to exercises identified with an asterisk (*) on the board prior to class. 

 

Textbook Exercises and Problems 6.1:  3-39 odd 17*, 37a*, (38)

Textbook Exercises and Problems 6.2:  (4b,d), 11-25 odd, 27*, 29*

Spiral-Bound Activity Book Connections 6.2 (p. 143):  (3b) See the example for 2.3 x 1.7 on the bottom of page 369 in the text. 

Textbook Exercises and Problems 6.3:  1-19 odd, 3*, (34)


Look at Polya's Problem Solving Process .

 

Look at a sample write up for 6.2 #4

Look at another sample write up for 6.2 #4

Look at a sample write up for 6.3 #34

Look at a sample write up for Activity Book #3b on p. 143


Assignment #2 - Due on Monday, Sept. 21 for Section 002 and Thursday, Sept. 17 for Section 004

 

Turn in written solutions only for the "regular exercises" and "problem solving exercises" whose numbers are enclosed in parentheses.  Write up your regular exercise solutions in a step-by-step manner as illustrated in the sample solutions for Examples K and L on page 387 in the text.  (Regular exercises are not designated by the "PS" icon.)  Write up your problem solving exercise solutions employing Polya's four-step process demonstrated in the problem problem solutions on pp. 405-406 and on pp. 425-426. (Problem solving exercises are designated by the "PS" icon.) 

 

Exercises and Problems 6.3: 1-23 odd, (2a), 30d*, 35, 37, (38)

Writing and Discussion (p. 411):  (4)

Read and work through Section 6.4 in "Mathematics for Elementary Teachers:  A Conceptual Approach."

Exercises and Problems 6.4:  1-21 all the odds, (14), (24), 33*, (38) For #38 illustrate Polya's problem solving steps.

Chapter 6 Test (pp. 422-423):  3, 7, 8, 9, 10, 11, 12, 13, 15, 16, 18, (20) 

 

Look at a sample write up for 6.3 #38

Look at a sample write up for 6.4 #38

 

Assignment #3 - Due on Wednesday, Sept. 23 for Section 002 and Tuesday, Sept. 22 for Section 004

 

Turn in written solutions only for the exercises whose numbers are enclosed in parentheses. Write up your problem solutions for "PS" exercises in a step-by-step manner employing Polya's four-step process.  Up to and including the due date for the assignment, for optional credit you are invited to place solutions to exercises identified with an asterisk (*) on the board prior to class. 

 

Read the indicated sections and work the indicated exercises. 

Exercises and Problems 9.1:  3-21 odd, (4), 22*, 23*, (24), 25*, (28) Hint for #28: Look at #22 and #23.

 

Look at a sample write up for 9.1 #24 (b,c)  Links activated Wednesday afternoon

Look at a sample write up for 9.1 #28

 

Assignment #4 - Due on Wednesday, Sept. 30 for Section 002 and Tuesday, Sept. 29 for Section 004

 

Turn in written solutions only for the exercises whose numbers are enclosed in parentheses. Write up your problem solutions for "PS" exercises in a step-by-step manner employing Polya's four-step process.  Read the sections 9.1 and 9.2 again and read pages  601-611 of section 9.3 and work the indicated exercises. 


Exercises and Problems 9.2:  3-19 odd, (4), (6), 7, (12), (18), (26)

Exercises and Problems 9.3:  2-5 all, (4), 8, 9

 

Look at an excellent student paper with some exercises from Assignment #4

Study Guide for Test #1 - Tuesday, October 6 for Section 004 and Wednesday, October 7 for Section 002

Review the "MATH 230-001 Course Objectives."

The test will cover objectives 6.1.1 through 6.4.5 and 6.* inclusive and objectives 9.1.1 through 9.2.1 and 9.* inclusive.  You should work and check as many of the suggested exercises as possible, and come to class sessions prepared to ask questions about those exercises or objectives you do not understand.  You may also e-mail questions to your instructor.

No questions concerning Test #1 will be answered after the last class prior to the test date.   No protractor, ruler, compass, or calculator can be used on the test.  (You may use your polygon pieces.)

Link to a copy of Test #1 given in Fall '06.

 

Assignment #5 - Due on Thursday, October 8 for Section 004 and on Monday, October 12 for Section 002

 

Do the following:

Construct models of five polyhedra using the patterns on Material Cards 29 and 30 in your spiral-bound activity book.  You may need to look at pictures of those polyhedra to see how the models should be assembled.  Bring those models to class on on the due date for the assignment.  Also, bring your spiral-bound activity book that day.  Take care in constructing your models, and be sure your models are already completed before you come to class.  If you do not have a spiral-bound activity book, or if you prefer to use different patterns from those in the activity book, go to the web site http://www.korthalsaltes.com/index.html and download alternative patterns for the Platonic solids.  Of course you could do a web search for "patterns for platonic solids" and download still other patterns for the platonic solids.

 

Assignment #6 - Due on Thursday, October 15 for Section 004 and on Monday, October 19 for Section 002

 

Write up your regular exercise solutions in a step-by-step manner so your thought process is clear.  (Regular exercises are not designated by the "PS" icon.)  Write up your problem solving exercise (PS) solutions employing Polya's four-step process demonstrated in the problem problem solutions on p. 381 and on p. 405-6.)  Problem solving exercises are designated by the "PS" icon.)  Up to and including the due date for the assignment, for optional credit you are invited to place solutions to exercises identified with an asterisk (*) on the board prior to class. 

 

Turn in written solutions only for the "regular exercises" and "problem solving exercises" whose numbers are enclosed in parentheses.

Exercises and Problems 9.3:  2-13 all except 4, 8, 9, 21*, 22, 27*, (28) (Instructions for #28 are on page 618 just above exercise #27.), 29*, (30), (34) .

Work through Section 9.4 in your textbook.

Exercises and Problems 9.4:  (2), 3-17 odd, (6), (10), 13*, (14), (18a), (30)

 

Link to sample write-ups for Exercises 9.3: #30 and #34

Link to sample write-ups for Exercises 9.4: #2 and #6

Link to sample write-ups for Exercises 9.4: #10 and #14

Link to sample write-ups for Exercises 9-4: #18 and #30

 

Assignment #7 - Due on Tuesday, October 20 for Section 004 and Wednesday, October 21 for Section 002

 

Work through Section 10.1 in your textbook

Exercises and Problems 10.1:  1-5 odd, 6, 11*, (10), 13*, (14), (20), (22), 31*

 

Link to sample write-ups for Exercises 10.1: #14 and #20

Link to sample write-up for Exercises 10.1: #22

 

Assignment #8 - Due on Thursday, October 22 for Section 004 and Monday, October 26 for Section 002

 

Read and work through Section 10.2 in the text.

Do Example B on page 671.

(Work #6 in the enrichment activity on page 684.  Turn in this exercise.)   

Exercises and Problems 10.2:  (6), 7a (Check your answer in the back of the book.), (8), (14), 13*, 15*, 17*, 19*,21* , (18), (22), (26), (40)

 

Link to sample write-ups for Exercises 10.2: #14 and #18b

Link to sample write-up for Exercises 10.2: #22

Link to sample write-up for Exercises 10.2: #26

Link to sample write-up for Exercises 10.2: #40

 

Test #2 - Tuesday, October 27 for Section 004 and Wednesday, October 28 for Section 002.

               Test #2 covers sections 9.1-9.4 and Sections 10.1-10.2)  No calculators; no notes.

 

You will need to have formulas for perimeter and area memorized so you can work exercises like those on the sheet from

Session 17.  (Test area problems will involve round numbers; so a calculator shouldn't be required.)

Look at a copy of Test #2 given Spring '06.  

(Our test would omit items #13, #14, and would only ask for the surface area in #19.)

Link to sample solutions for Test #2

 

 

 

Assignment #9 - Due on Tuesday, November 3 for Section 004 and Wednesday, November 4 for Section 002

 

Read and work through Section 10.3 in the text.

Exercises and Problems 10.3:  5-13 odd, (8,  See instructions above #7), (12,  See instructions above #7), (14,  See instructions above #13.), (32) For #32 take a look at #28.

Activity Set 10.3 in Spiral-Bound Activity Book:  (5)

 

Link to sample write-ups for Exercises 10.3: #12 and #14

Link to sample write-ups for Exercises 10.3: #8, #32 and Activity Set 10.3#5

 

Assignment #10 - Due on Tuesday, November 10 for Section 004 and Wednesday, November 11 for Section 002

 

Look at the different problem solving strategies illustrated in Section 1.1.

Carefully study the sample problem that is stated, "Find an easy method for computing the sum of consecutive whole numbers from 1 to any given number."

Exercises and Problems 1.1:  (2, Illustrate Polya's problem solving process)

Read and work through Section 1.2.

Exercises and Problems 1.2:  3, 5, (6) Look at #5, 7, (8) Look at #7, (24), (26), (32 See instructions above #31.))

 

Please remember to submit an example of your best work.  Papers are expected to be neat, well-organized, and correct.  Clearly communicate your thought processes and state your conclusions using complete sentences.

 

Look at a sample solution for 1.1/#2.

Look at a sample solution for 1.2/#6.

Look at another sample solution for 1.2/#6

Look at a sample solution for 1.2/#8.

Look at another sample solution for 1.2/#8.

 

Assignment #11 - Due on Tuesday, November 17 for Section 004 and Wednesday, November 18 for Section 002

 

Ex/Prob Set 1.3:  (36) 

Ex/Prob Set 2.2:  (12), (38)

(Write up the following exercise:)

(Exercise)  Consider the following three sequences.  One is an arithmetic sequence; one is geometric, and

one is quadratic.  Draw a very nice graph of each sequence and then classify each

sequence by type, identify F(8) and show how to determine both a difference equation and an explicit functional

equation for each sequence.

(a)  

n 0 1 2 3 4 5 6 7
F(n) 5 10 19 32 49 70 95 124

 

(b)

n 0 1 2 3 4 5 6 7
F(n) 3 6 12 24 48 96 192 384

 

(c)

n 0 1 2 3 4 5 6 7
F(n) 4.00 5.50 7.00 8.50 10.00 11.50 13.00 14.50

 

Look at a sample solutions for 1.3/#36

Look at a sample solutions for 2.2/#12

Look at a sample solutions for 2.2/#38

Look at a sample solutions Exercises (a), (b), and (c) above.  (Graphs not included.)

 

Assignment #12 - Due on Monday, November 23 for Section 002 and Tuesday, November 24 for Section 004

 

Carefully study the material on "Scatter Plots" on pp. 437-438 in your text.

In particular, study Examples E and F.

Ex/Prob Set 7.1:  (36), (38)  Be sure to display your graphs and write out the equations of your trend lines.

 

Link to sample solutions for these exercises.

 

Assignment #13 - Due on Wednesday, December 2 for Section 002 and on Thursday, December 3 for Section 004

 

Exercise 0.)  Complete the Grade Calculation Worksheet with information to date and turn it in with this assignment.

(Exercise 1.)  (Write up this exercise.)  These days it is possible to lease just about any car. For example, for the modest fee of $1500 down plus $750 per month you can drive a Jaguar. Unfortunately, those charges add up.

a) What pattern will appear in a table showing total leasing cost as a function of number of months in the lease? 

Lease time    0   1   2   3   4   5   6   7   8
Total cost
 
b) What pattern do you expect in a graph relating lease time and total payment?
c) What equation will give an appropriate rule relating length of lease (x) and total payment (y)?
 

(Exercise 2.)  (Write up this exercise.) In 1975 a new Ford Mustang car had a base price of $4,906. In 1981 a comparable car had a base price of $7,900; in 1987 a base price of $9,750; and in 1993 a base price of $13,245.
(a). On graph paper, make a plot of the sample (year, price) data and draw a line that fits the pattern of the data well. (Hint: Use time beginning with 1975 as 0.) Find an equation in the form y = mx + b for that model line and explain what m and b tell about the situation.
(b). Use your linear model from (a) to estimate base price for Ford Mustangs in 1978, 1984, 1990, and 1994.

(Exercise 3)  (Write up this exercise.)  One of the amazing properties of mathematical ideas is that patterns discovered in one context turn up in quite different and unexpected places. Then calculations done the first time can be applied to the new situations. This recurrence of fundamental patterns is an especially impressive property of exponential models.

For example, drugs are a very important part of the human health equation. Many drugs are essential in preventing and curing serious physical and mental illnesses; many other drugs cause damaging addiction and physical or mental impairment.



For the 5 million Americans of all ages who suffer from diabetes, insulin is an extremely valuable drug. To provide that essential hormone, when the body's pancreas production fails, diabetics take the drug insulin. However, once in the blood stream, insulin begins breaking down into other chemicals and soon passes from the body. A typical pattern of decrease for insulin in the blood is shown in the following graph.


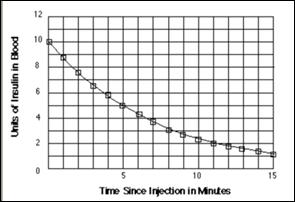
(a)  Medical scientists are usually interested in the time is takes for a drug to be reduced to one half of the original dose. They call this time the half-life of the drug. What appears to be the half-life of insulin?

The pattern of decay shown on the graph for insulin can be modeled well by an exponential equation in the form y = A(b)x .

(b)  Enter five or six data points from the given graph and calculate the ratios of successive terms to the preceding terms.  Choose a particular ratio to represent the “typical” pattern of change you observe, and use that ratio to formulate both a difference equation and a functional equation to approximate the relationship between the amount of insulin in the blood and time elapsed since injection.

(c) Test your rules and describe how well your models fit the data in the graph.

(d) Explain what the values of A and b tell about the action of insulin in the blood.

Link to a student's work on exercises 1 and 3

Link to tips for exercises 1 and 2

Link to another solution for exercise 3

 

Study Guide for Test #3 - Test #3 Monday, December 7 for Section 002; Tuesday, December 8 for Section 004.

Test #3 Will cover the course objectives listed below including Section 10.3 in the text.

 

 

Test #3 will address objectives 10.3.1, 10.3.2, 1.2.1, 2.2.1, 2.2.2, 2.2.3, M.1-M.8  (Calculators are allowed.) You may find the course objectives at

 http://faculty.salisbury.edu/~dccathcart/Math230/objectiv04.html  

 

A good way to prepare for a test is to work many of the exercises suggested with the objectives.  Also, as you work each assignment, work the suggested odd numbered exercises and check your answers by looking in the back of the text.  Many test items will look like those exercises assigned but not collected.  Problem solving ability, persistence, and creativity are evaluated on the papers you turn in each week.  The more routine knowledge, skill, and concept-related objectives are evaluated on the tests.

 

Link to sample solutions for Test #3

 

Link to some practice problems related to surface area and volume.
Link to a sample test - Test #3, Spring 2004.    Be aware that our test will include a surface area and volume exercise.  Note that solutions will not be provided for items on this sample test.  Compare your solutions with those of another individual.  Keep studying until you are confident in your solutions. You may use a calculator on Test #3.  In addition to working the practice test, you need to be sure you can work problems like those on the assignments since Test #2 and like those we have worked in class since Test #2.  Link to another sample test - Test #3, Fall 2006.  

 

Final Exam - Monday, Dec. 14 at 8:00 am for Section 004 and Wednesday, Dec. 16 at 4:15 pm for Section 002

The final exam is comprehensive and will address the course objectives.  You may use a calculator on the final exam.
 

Review Test #1, Test #2, and Test #3 as you prepare for the final exam.  Be sure you can work items like those on
each of the three tests. There may be an item of the final asking you to demonstrate use of Polya's problem solving process.

Link to a grade calculation worksheet.

Look at the " Guidelines for Written Work ."
Return to the top of this page .
Look at the homepage for this course .